Controllo Statistico della Qualità: alcuni casi studio

Author

Nicola Menegon

Caso 1: Sulla resistenza dei laminati plastici

x <- scan("~/Uni/Controllo/Datasets/plastic-strength")
str(x)
 num [1:125] 140 139 144 141 136 ...

I dati corrispondono a 25 gruppi di 5 misurazioni di alcuni laminati plastici per una misura di resistenza alle flessioni trasversali. Una visualizzazione più sensata dei dati è una matrice in cui ogni colonna indica un sottogruppo

summary(x)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  133.7   138.5   139.8   139.9   141.4   144.1 
d <- matrix(x, 5, 25)

Ci chiediamo se vi siano state variazioni della resistenza media del prodotto nel tempo.

library(dfphase1)
phase1Plot(d)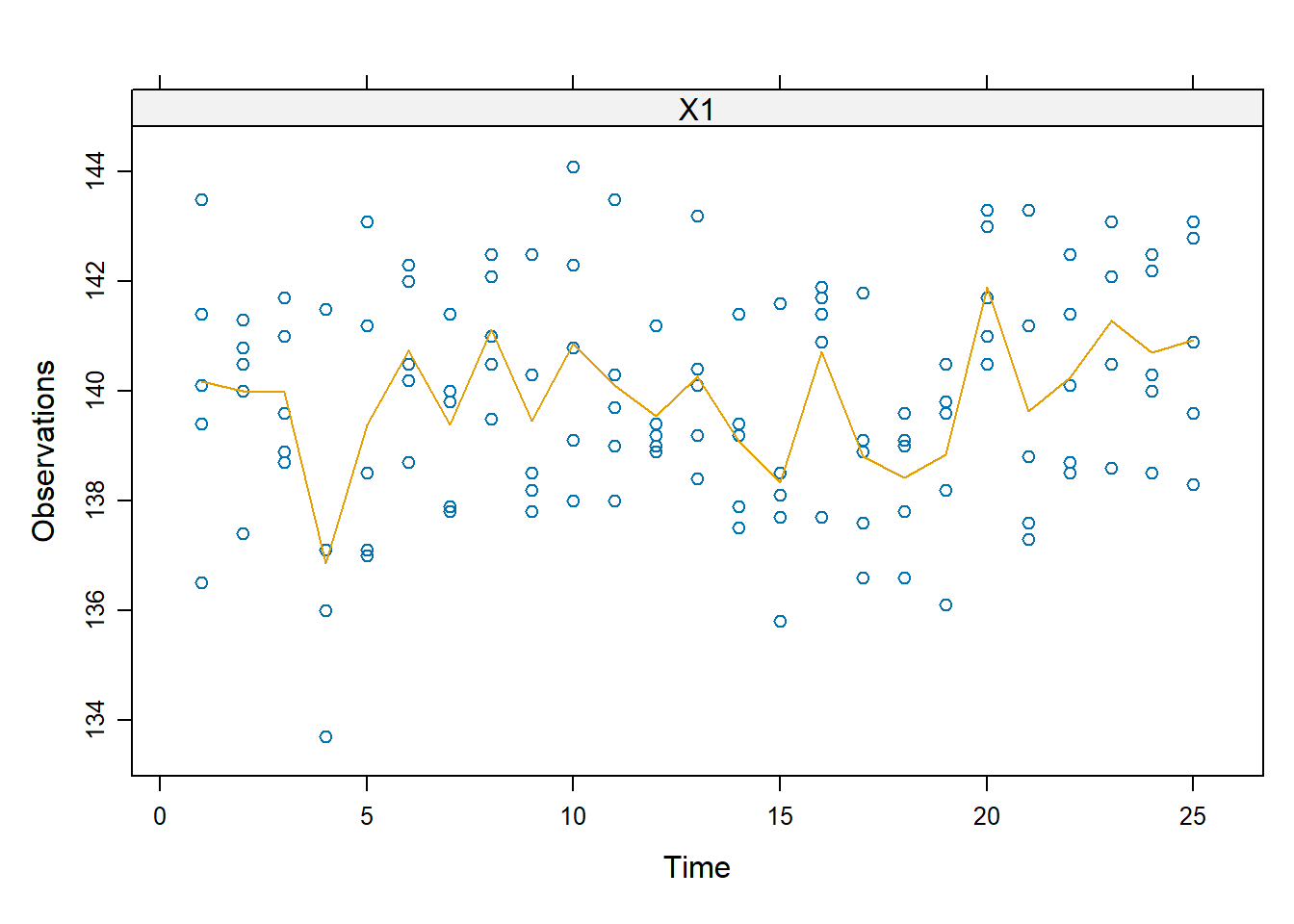

Assumendo normalità, calcoliamo e disegniamo i limiti di controllo di Shewhart a livello $ = 0.10 $.

FAP <- 0.10
L <- shewhart.normal.limits(m = 25, n = 5, stat = "Xbar", FAP = FAP)
L
     90% 
2.857715 
m <- shewhart(d, stat = "Xbar", limits=L)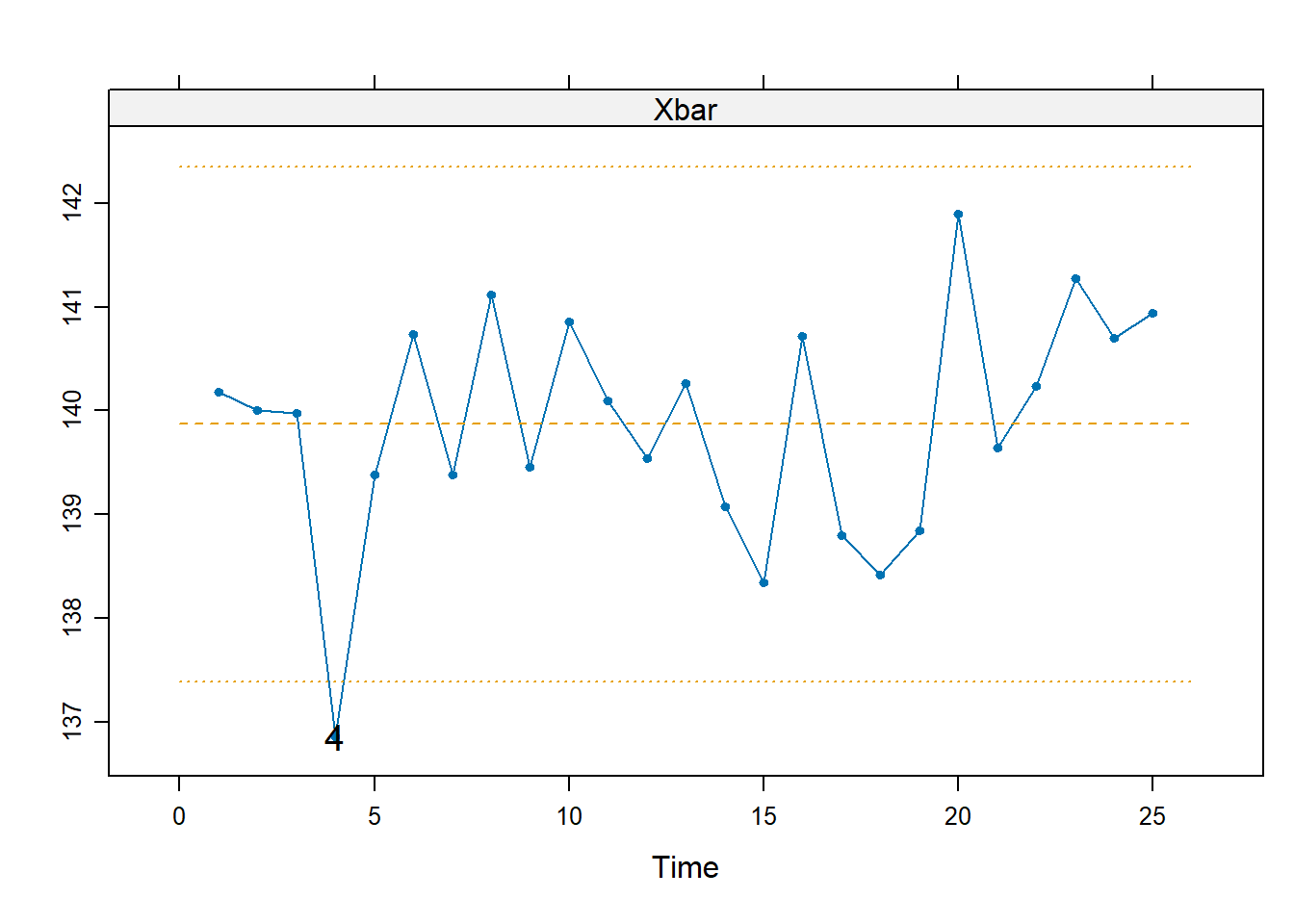

Emerge un allarme per il quarto turno di produzione. In effetti, ciò era dovuto a una maggiore viscosità delle resine registrata in quella giornata, dunque l’allarme segnalato era plausibilmente dovuto a un cambiamento reale nella qualità della produzione.

Si noti che shewhart.normal.limits() calcola, via simulazione del quantile, i limiti di controllo per una normale con data numerosità. Successivamente, shewhart() mostra il grafico. In realtà, quest’ultima produce lo stesso esatto risultato anche senza passargli il termine limits=L, ma a noi piace complicarci le cose.

È buona cosa ricalcolare i limiti di controllo solo sulle osservazioni in controllo

L <- shewhart.normal.limits(m = 24, n = 5, stat = "Xbar", FAP = FAP)
m <- shewhart(d, stat = "Xbar", subset = -4)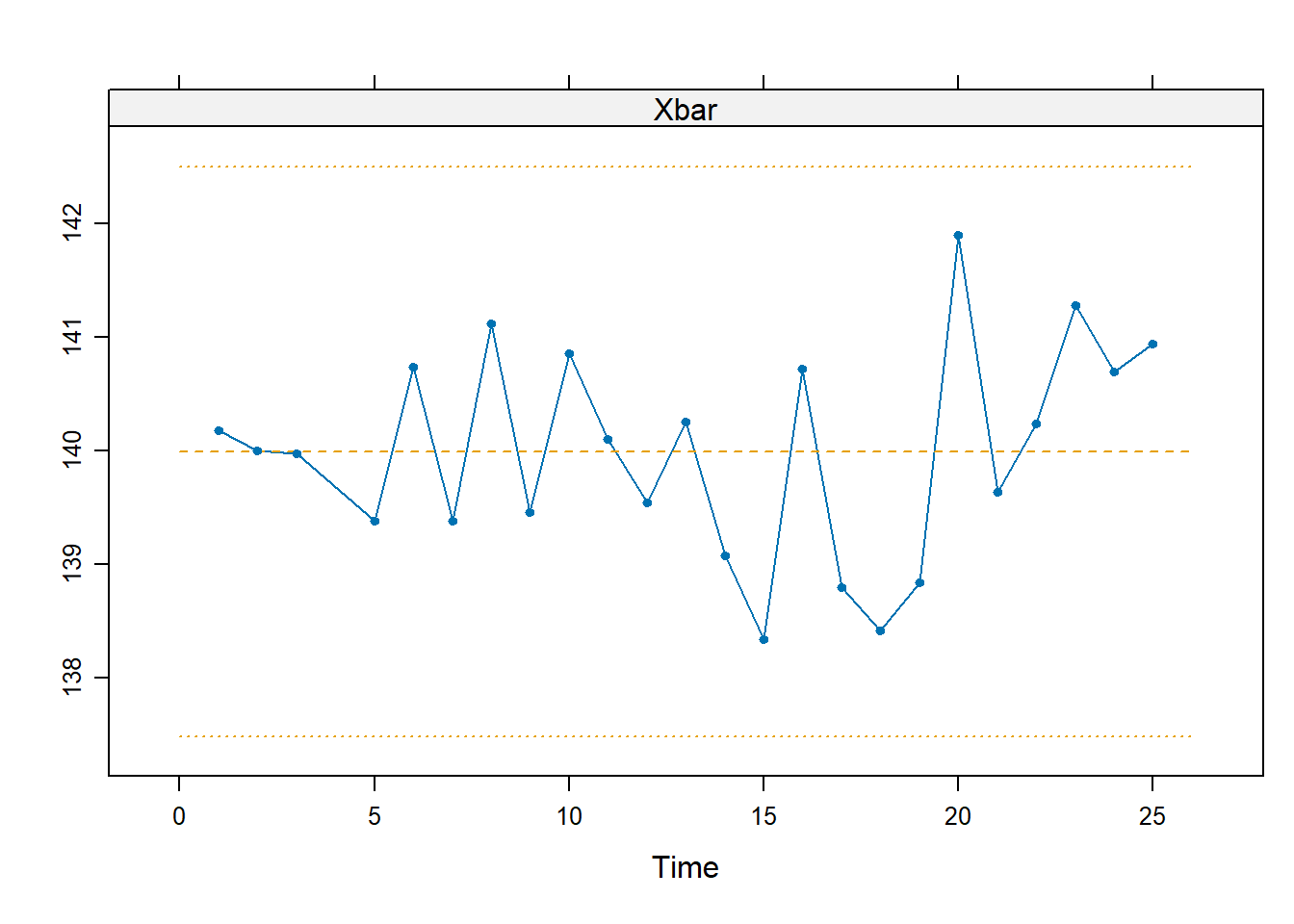

Dei rimanenti campioni nessuno supera i limiti, dunque è ragionevole assumere che abbiano tutti la stessa media (e dunque che stimino correttamente la media del processo in controllo (IC)).

Si procede in modo del tutto analogo per la carta di controllo S.

L <- shewhart.normal.limits(m = 25, n = 5, stat = "S", FAP = FAP)
shewhart(d, stat = "S", limits = L)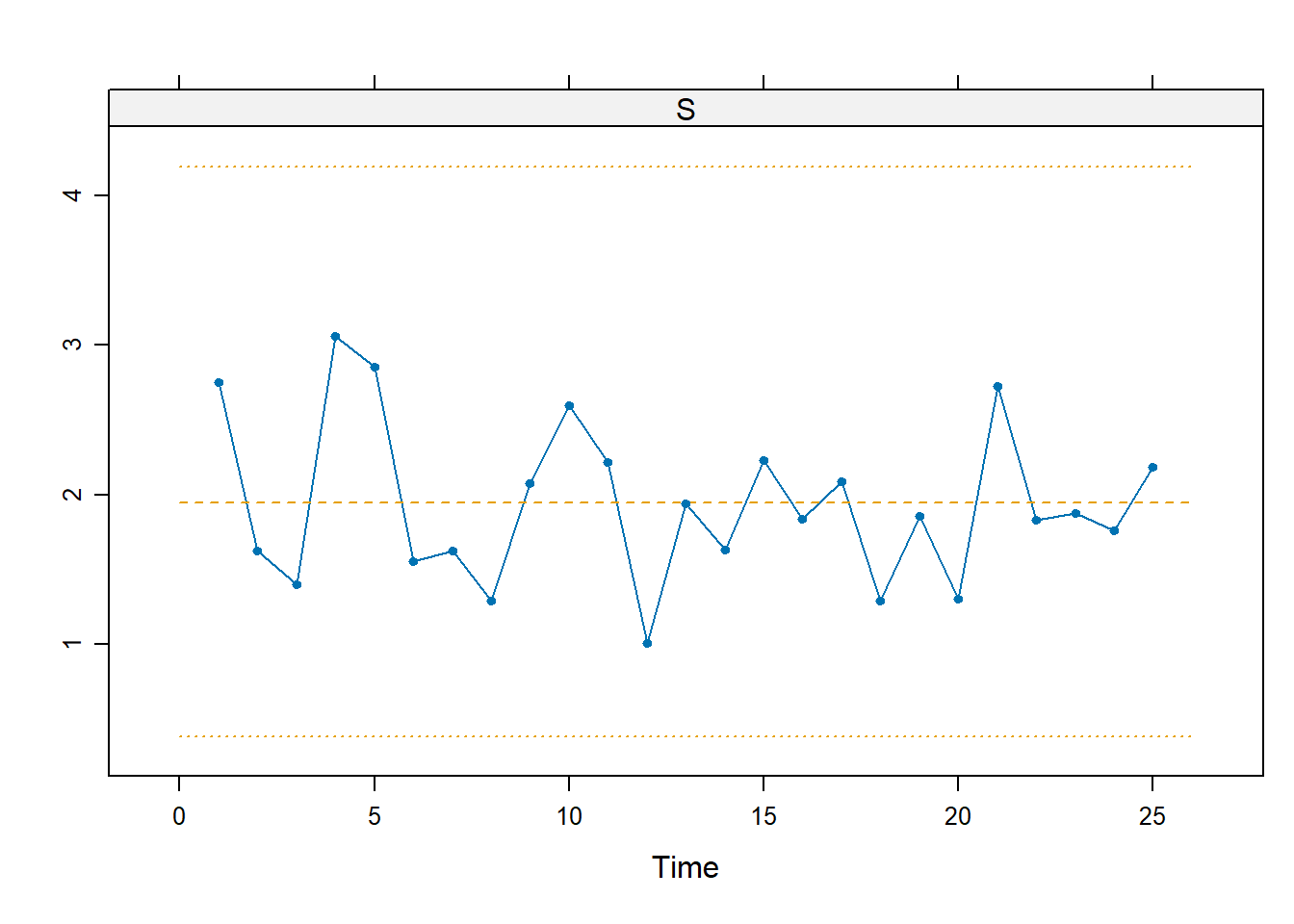

Tutti i nostri procedimenti si basano sull’assunzione parametrica di normalità. Possiamo verificarla solo sui sottogruppi IC, per i quali assumiamo uguale media e varianza

x <- as.numeric(d[,-4])
qqnorm(x)
qqline(x)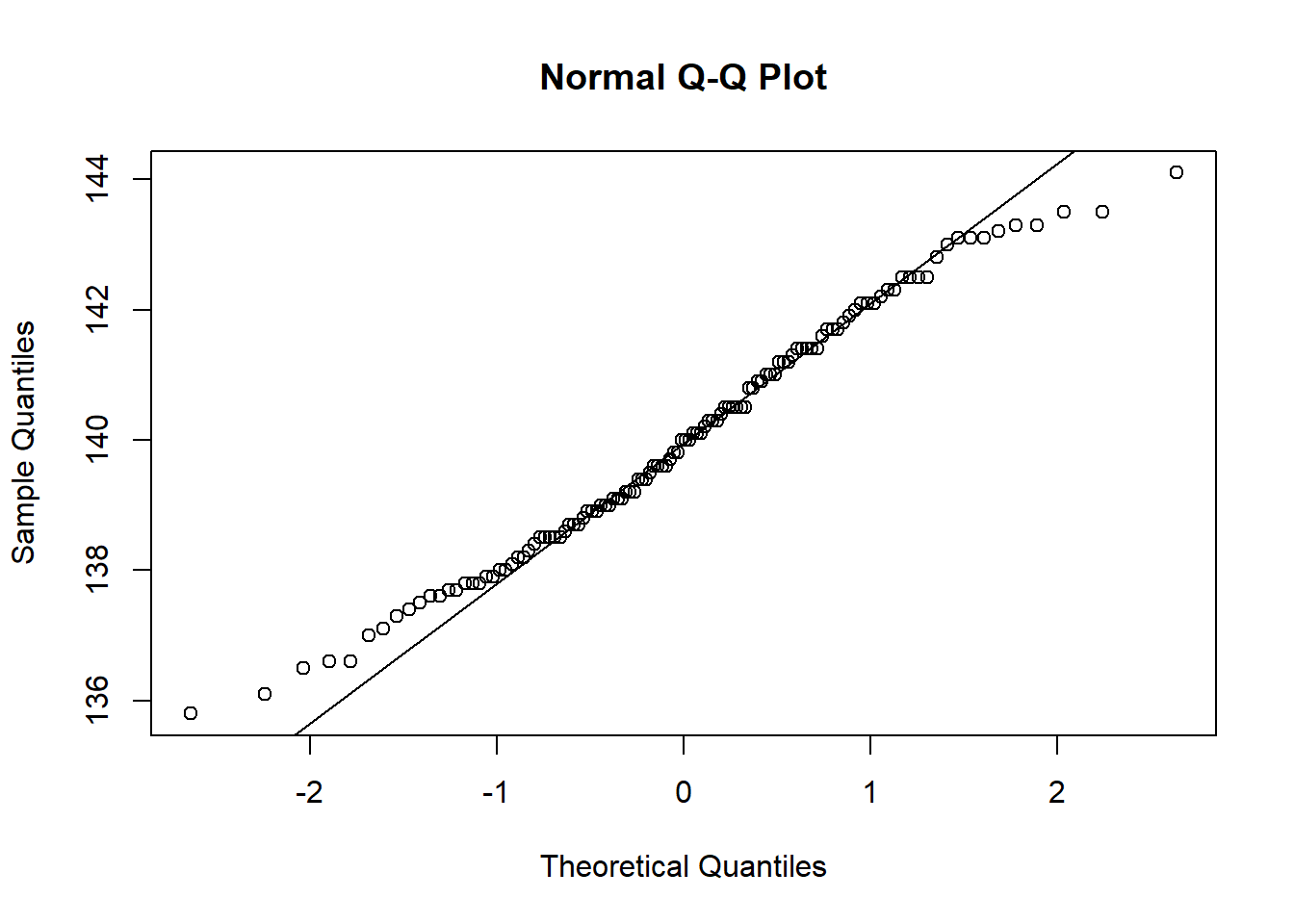

shapiro.test(x)

    Shapiro-Wilk normality test

data:  x
W = 0.98444, p-value = 0.1829

Non c’è particolare evidenza contro l’ipotesi di normalità.

Caso 2: Le etichette della passata di pomodoro le vogliamo perfette!

x <- scan("~/Uni/Controllo/Datasets/passata")
str(x)
 num [1:49] 4 4 6 8 8 4 4 5 1 7 ...

L’oggetto x contiene il conteggio del numero di bottiglie non conformi nel giorno \(t\). Si ha, quindi, che \[ x_t \sim Bin(200, p_0), \quad t = 1,\ldots,49 \]

Come statistica di controllo possiamo scegliere \[ \hat{p}_t = \frac{x_t}{n} \overset{\cdot}{\sim} N(p_0, \frac{p_0(1-p_0)}{n}) \]

Da cui discendono banalmente i limiti di controllo. Per la stima, \(\hat{p}_0 = \frac{1}{m} \sum_{t=1}^{m} \hat{p}_t\).

Per il calcolo di L, è opportuno procedere per simulazione, stimando così i quantili della distribuzione di \[ G = \max_{t = 1, \ldots, m} \left| \frac{\hat{p}_t - \hat{p}_0}{\sqrt{\frac{\hat{p}_0 (1 - \hat{p}_0)}{n}}} \right| \]

Caso 3: L’alluminio dei blu-ray deve avere lo spessore giusto!

Sui blu-ray viene steso uno strato di alluminio che permette la lettura dei dati incisi. L’azienda utilizza a questo fine 3 diversi spruzzatori. Per 27 lotti consecutivi vengono campionati 3 pezzi, uno per spruzzatore.

x <- scan("~/Uni/Controllo/Datasets/blu-ray")
str(x)
 num [1:81] 439 443 458 433 449 460 437 446 452 441 ...
d <- matrix(x, 3, 27)
L <- shewhart.normal.limits(m = 27, n = 3, stat = "Xbar")
m <- shewhart(d, stat = "Xbar", limits = L)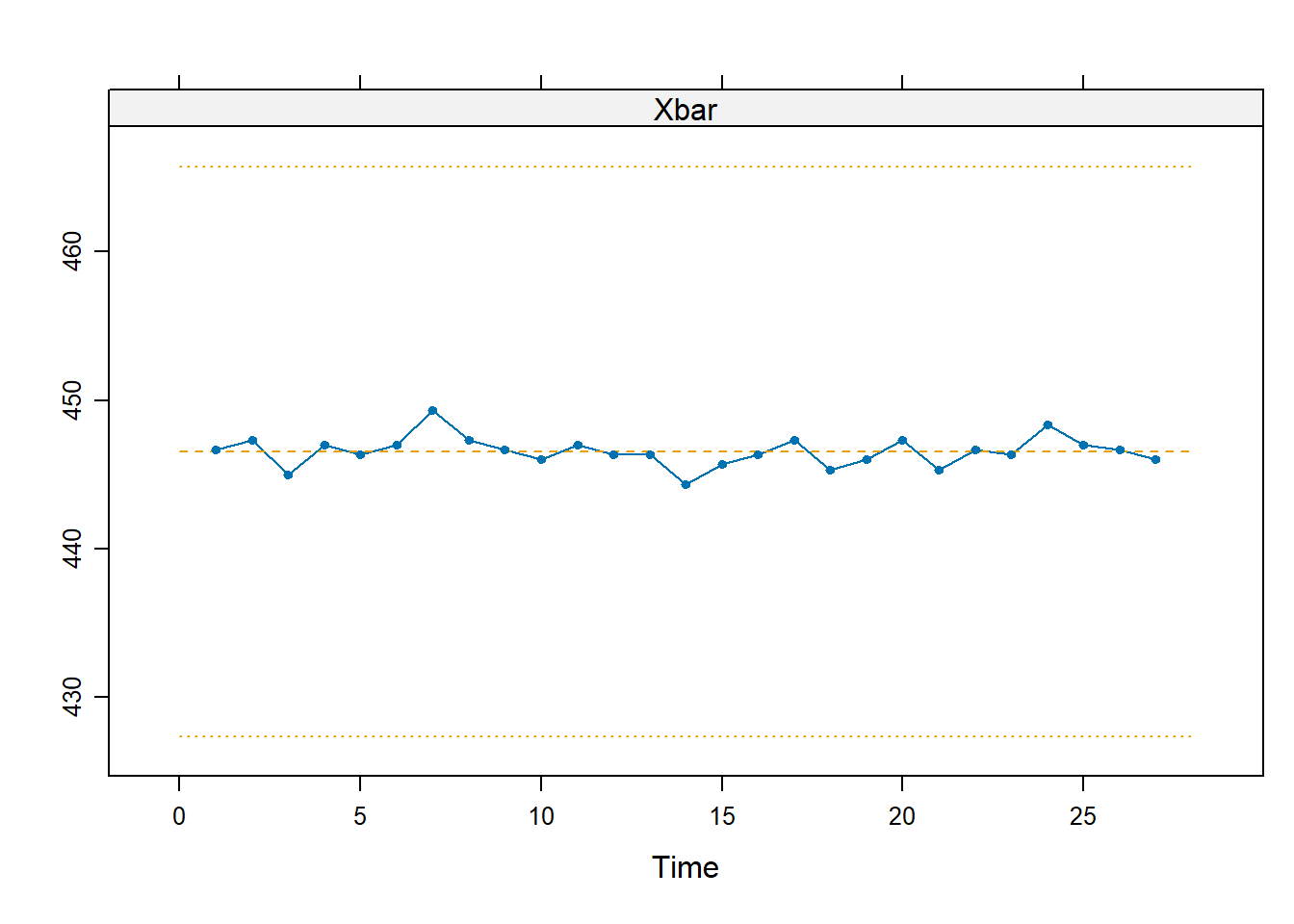

Non vengono segnalati allarmi. Tuttavia, le medie sono eccessivamente lontane dai limiti di controllo. Ciò in genere indica che la varianza interna ai sottogruppi (quindi, nel nostro caso, tra gli spruzzatori) è superiore a quella tra i sottogruppi (ovvero tra un lotto e l’altro).

In effetti, questa ipotesi è confermata da quanto segue

phase1Plot(d)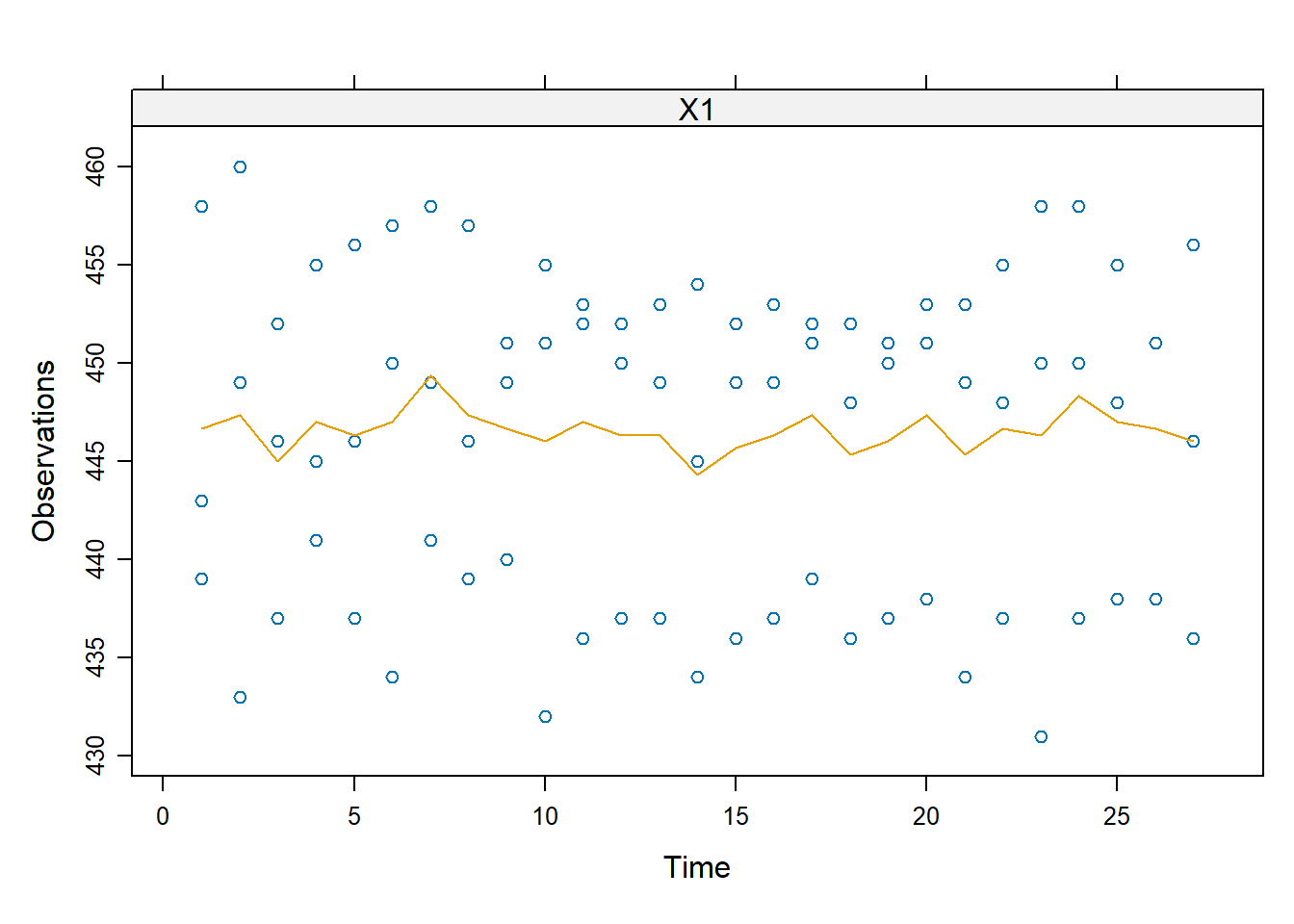

matplot(t(d), type = "b", col = 2:4)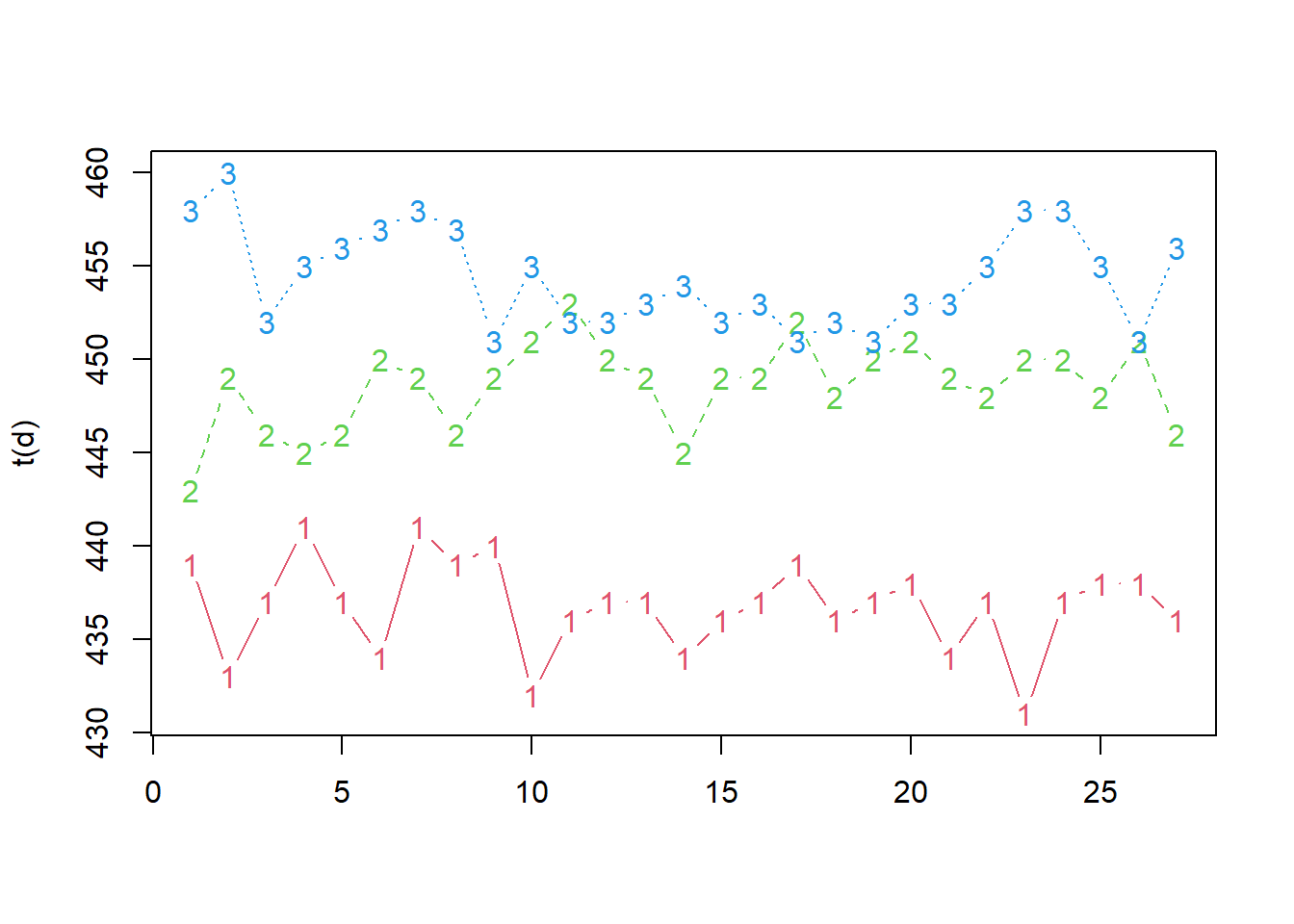

I tre spruzzatori sono abbastanza precisi nelle loro performance, ma sono tarati su medie diverse tra loro. Se gli spruzzatori 1 e 3 fossero tarati sulla stessa media di 2 avremmo

ora <- as.numeric(d)
dopo <- as.numeric(d - rowMeans(d) + mean(d[2, ]))
matplot(t(matrix(dopo, 3)), type="b", col=2:4)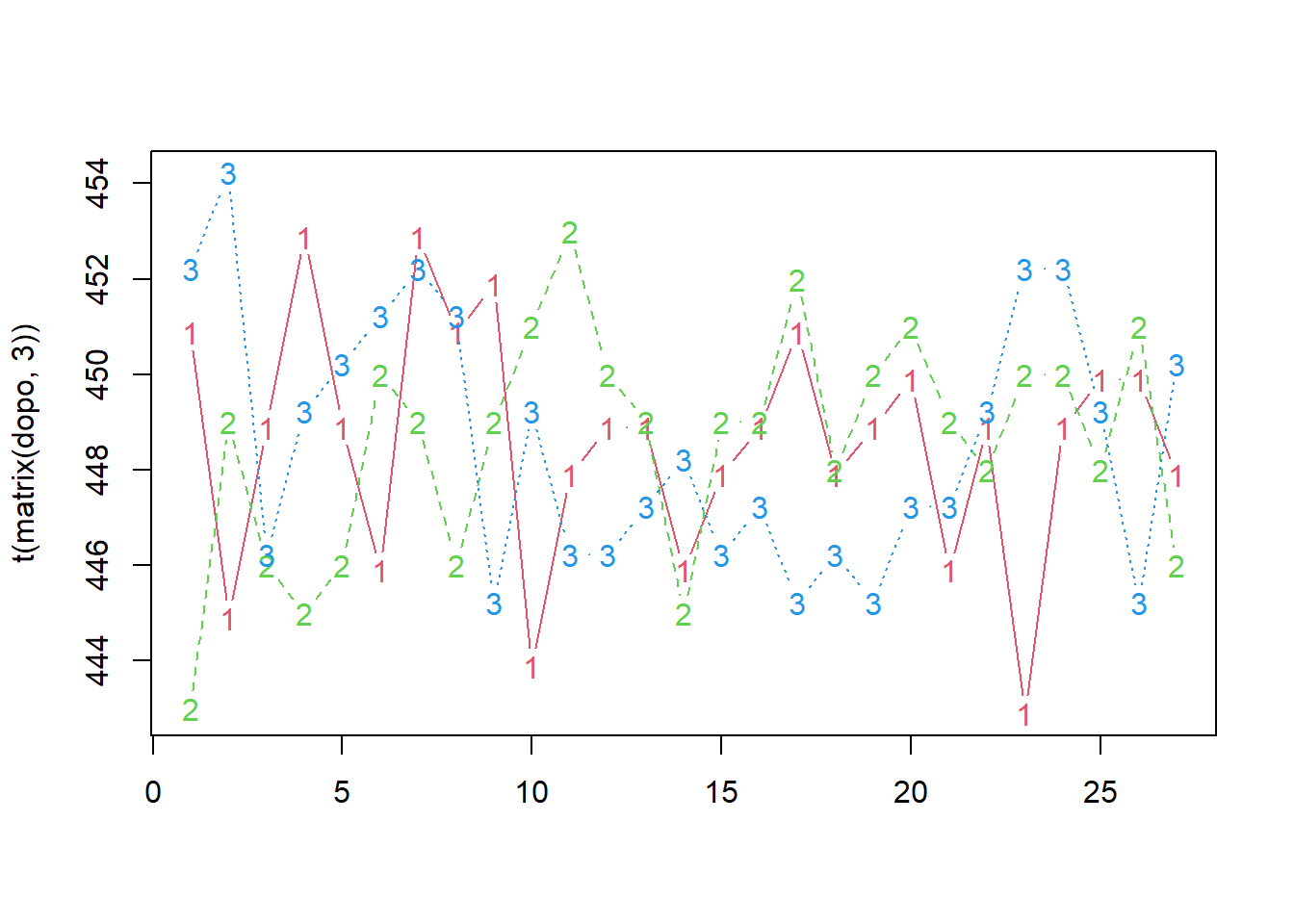

boxplot(ora, dopo)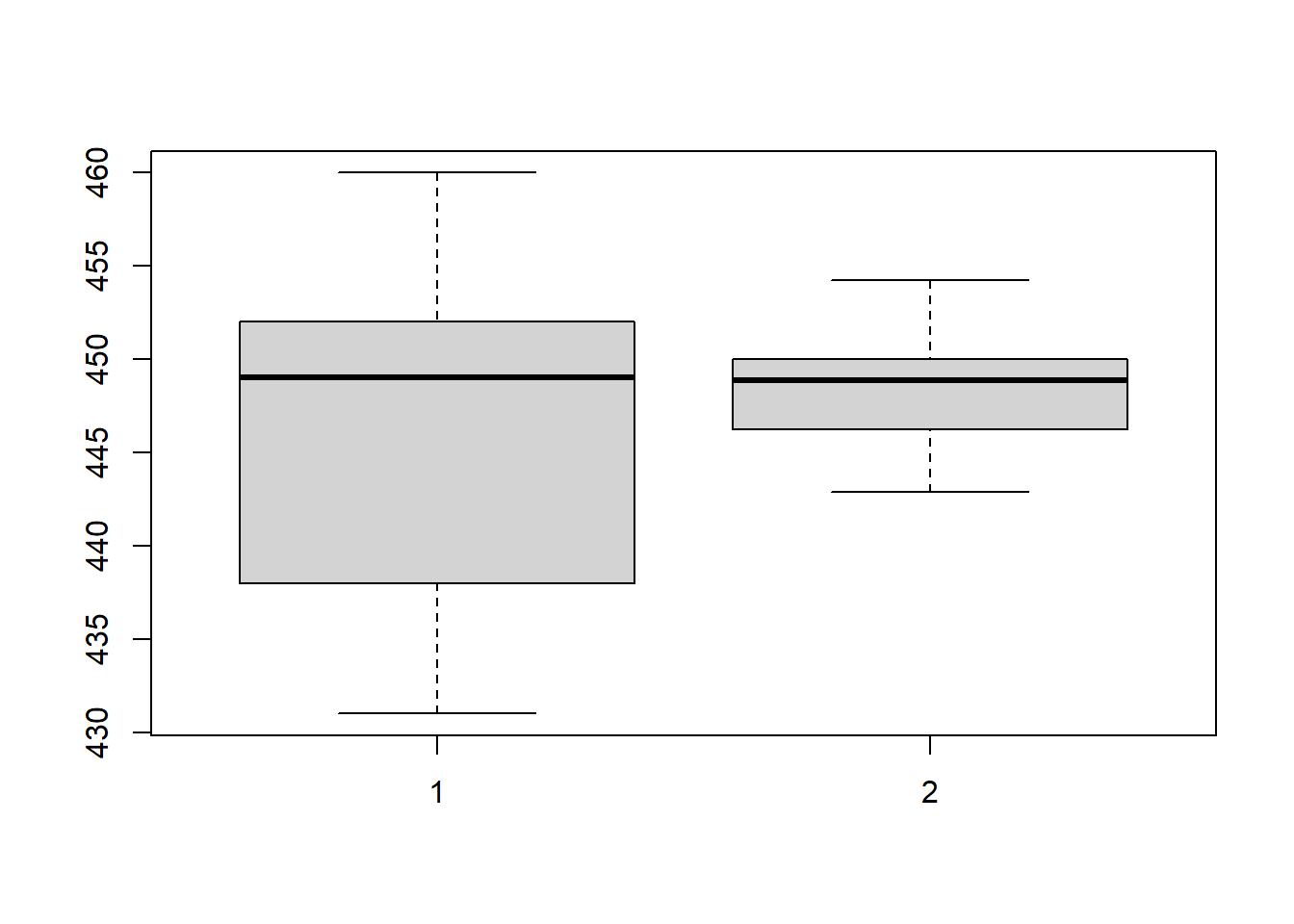

Che è la situazione che vorremmo. Da qqplot e test non emergono indicazioni contro l’ipotesi di normalità. La morale è che non basta guardare se i punti stanno dentro o fuori dai limiti.

Caso 4: Su di un broncodilatatore a rilascio lento

I dati provengono da un’industria farmaceutica che produce compresse che rilasciano lentamente un broncodilatatore. Nella fase di produzione queste devono essere rivestite da una certa membrana semi-permeabile, in modo che il farmaco fuoriesca lentamente da un buco fatto da un laser.

R <- read.table("~/Uni/Controllo/Datasets/tablet")
str(R)
'data.frame':   460 obs. of  14 variables:
 $ lotto : int  1 1 1 1 1 2 2 2 2 2 ...
 $ ora.0 : int  0 0 0 0 0 0 0 0 0 0 ...
 $ ora.1 : num  0.1 0.09 0.09 0.07 0.07 0.11 0.08 0.08 0.07 0.09 ...
 $ ora.2 : num  0.17 0.18 0.2 0.15 0.15 0.19 0.17 0.17 0.15 0.17 ...
 $ ora.3 : num  0.25 0.27 0.26 0.23 0.23 0.27 0.26 0.26 0.25 0.26 ...
 $ ora.4 : num  0.34 0.35 0.37 0.32 0.32 0.36 0.36 0.33 0.34 0.35 ...
 $ ora.5 : num  0.43 0.42 0.45 0.4 0.41 0.44 0.42 0.4 0.42 0.44 ...
 $ ora.6 : num  0.51 0.51 0.53 0.5 0.51 0.51 0.52 0.47 0.52 0.52 ...
 $ ora.7 : num  0.59 0.61 0.61 0.59 0.58 0.6 0.61 0.56 0.59 0.59 ...
 $ ora.8 : num  0.7 0.69 0.69 0.68 0.65 0.69 0.69 0.63 0.66 0.67 ...
 $ ora.9 : num  0.79 0.77 0.78 0.75 0.72 0.79 0.77 0.73 0.72 0.75 ...
 $ ora.10: num  0.88 0.85 0.86 0.81 0.78 0.88 0.84 0.81 0.8 0.83 ...
 $ ora.11: num  0.99 0.93 0.97 0.89 0.88 0.96 0.92 0.91 0.88 0.92 ...
 $ ora.12: int  1 1 1 1 1 1 1 1 1 1 ...
ora <- 0:12
matplot(ora, t(R[, -1]), type = "l", ylab = "rilascio cumulato (%)")
abline(0, 1/12, col="black", lwd=4, lty=3)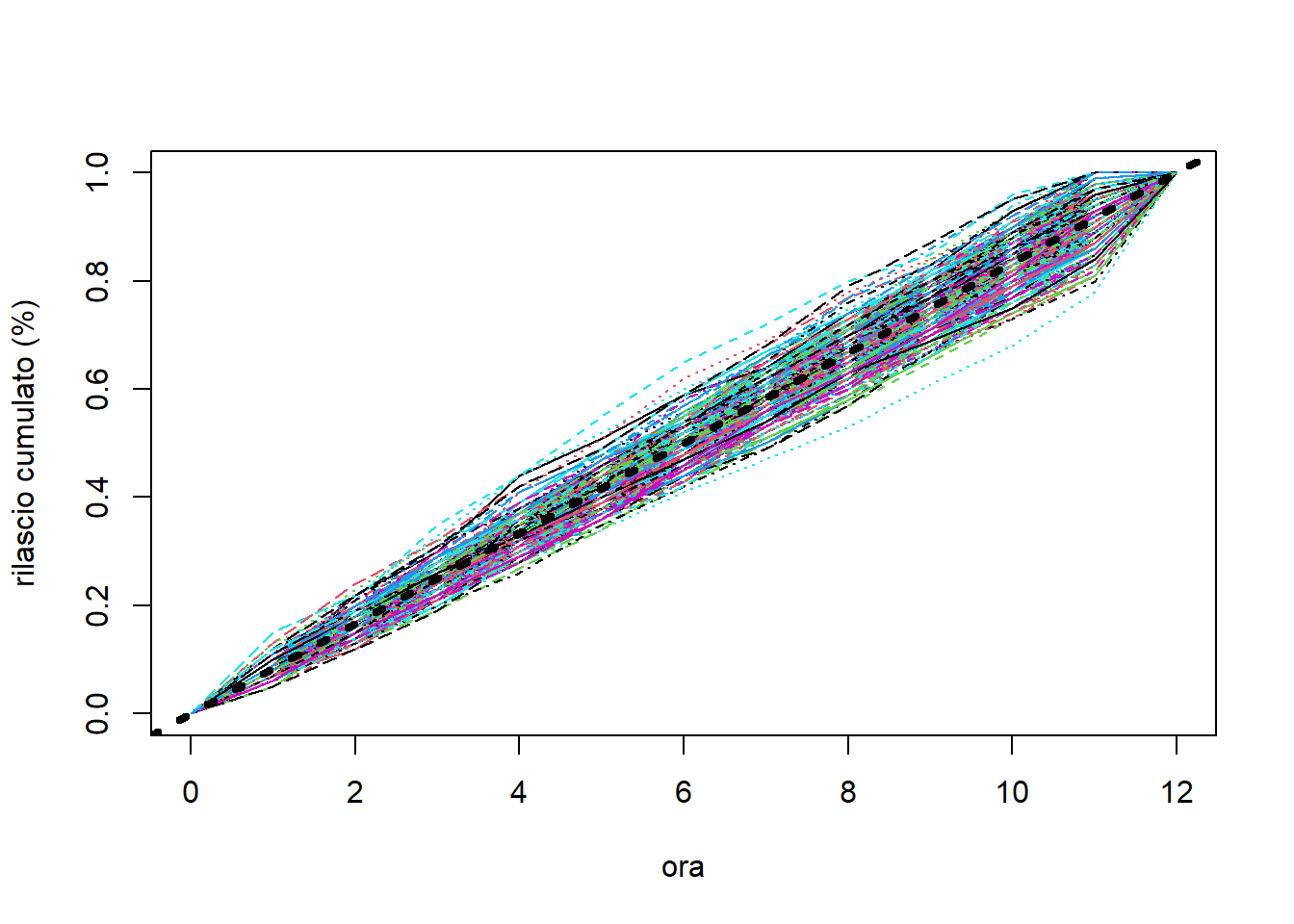

Vorremmo che tutte le compresse seguissero l’andamento della retta tratteggiata nera. L’azienda intende valutare la distanza tra traiettoria effettiva per la \(j\)-esima compressa, rappresentata da \(r_j, j=0,...,12\) e quella ideale tramite le statistiche \[ U = \max_{j = 1, \ldots, 10} \, (r_j - r_{j-1}) \quad \text{e} \quad V = \min_{j = 1, \ldots, 10} \, (r_j - r_{j-1}) \]

Per valutare l’andamento utilizziamo questa volta un approccio basato su RS/P. Questo perché l’ipotesi di normalità è dubbia e impedisce l’utilizzo delle carte di Shewhart.

D <- R[, 3:14] - R[, 2:13] # rilasci orari
u <- apply(D[, 1:10], 1, max)
v <- apply(D[, 1:10], 1, min)
library(dfphase1)
rsp(matrix(u, 5))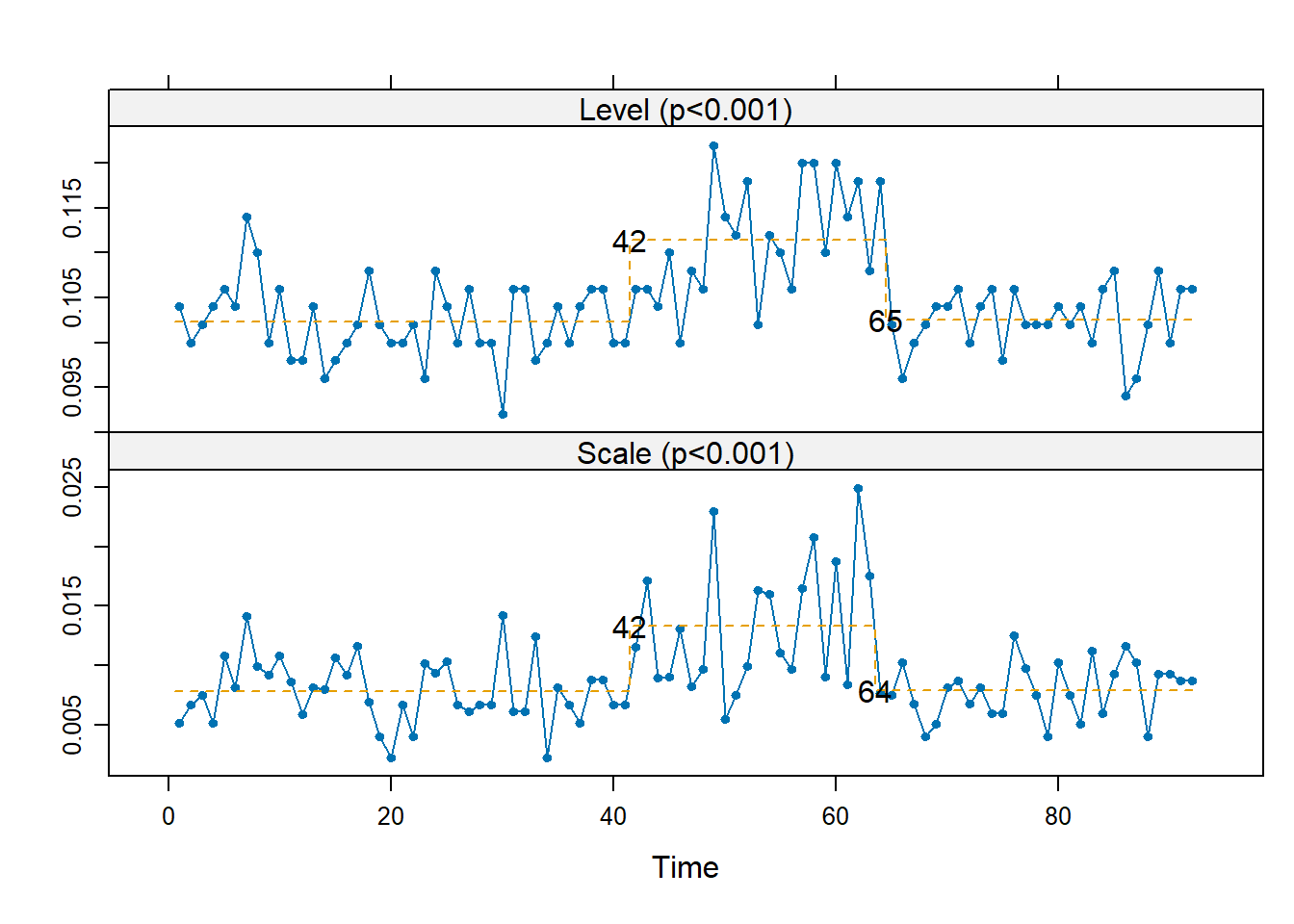

rsp(matrix(v, 5))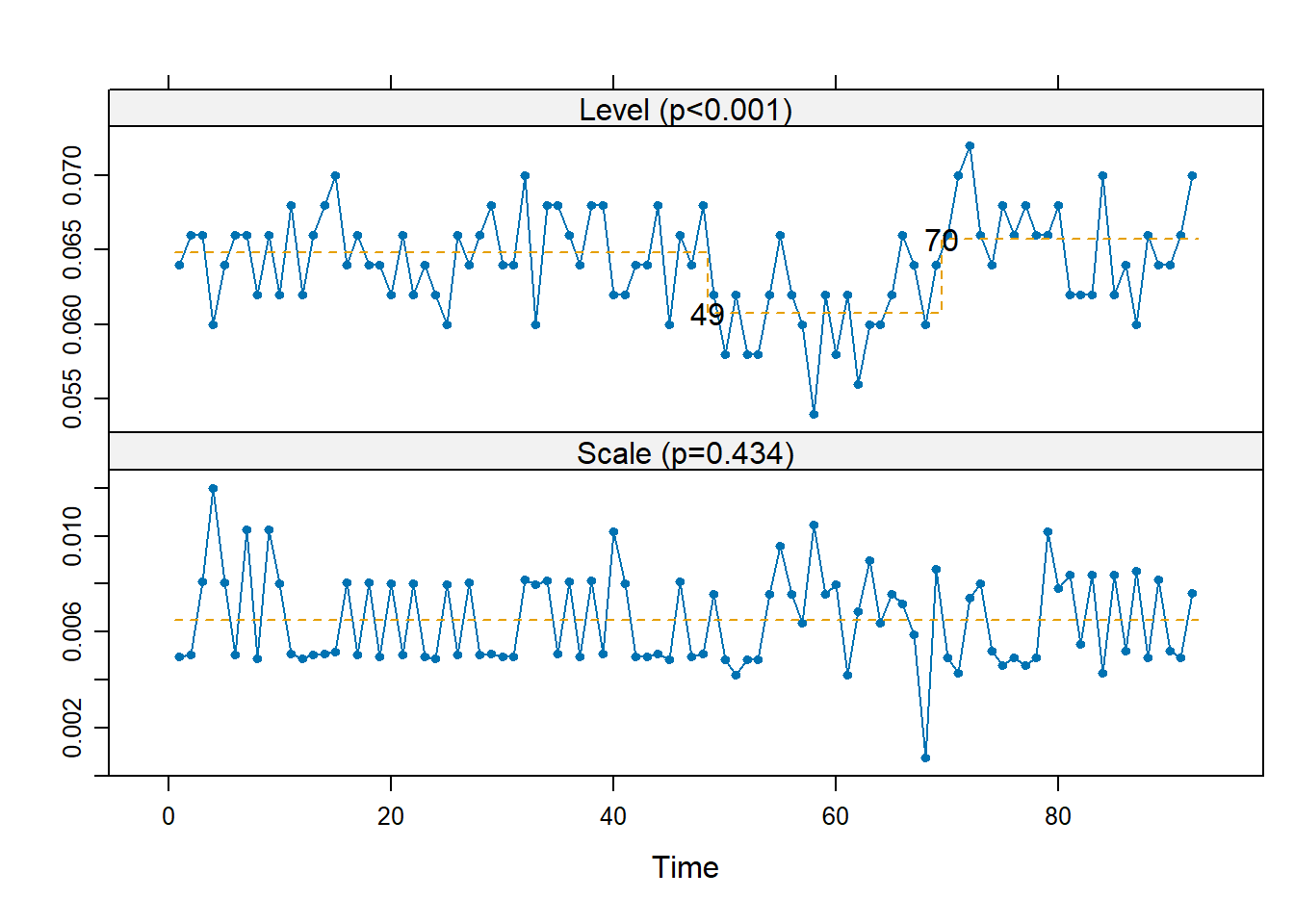

Sembra esserci un effetto transitorio tra i lotti 42-49 e 64-70 in cui sembrano essere aumentate media e variabilità di \(U\) e diminuita la media di \(V\).

IC <- (R$lotto <= 41) | (R$lotto >= 70)
OC <- (R$lotto >= 49) & (R$lotto <= 63)
par(mfrow=c(3,4), mar = c(1, 1, 1, 1), oma = c(0, 0, 0, 0))
for (i in 1:12) boxplot(D[IC, i], D[OC, i], main = i)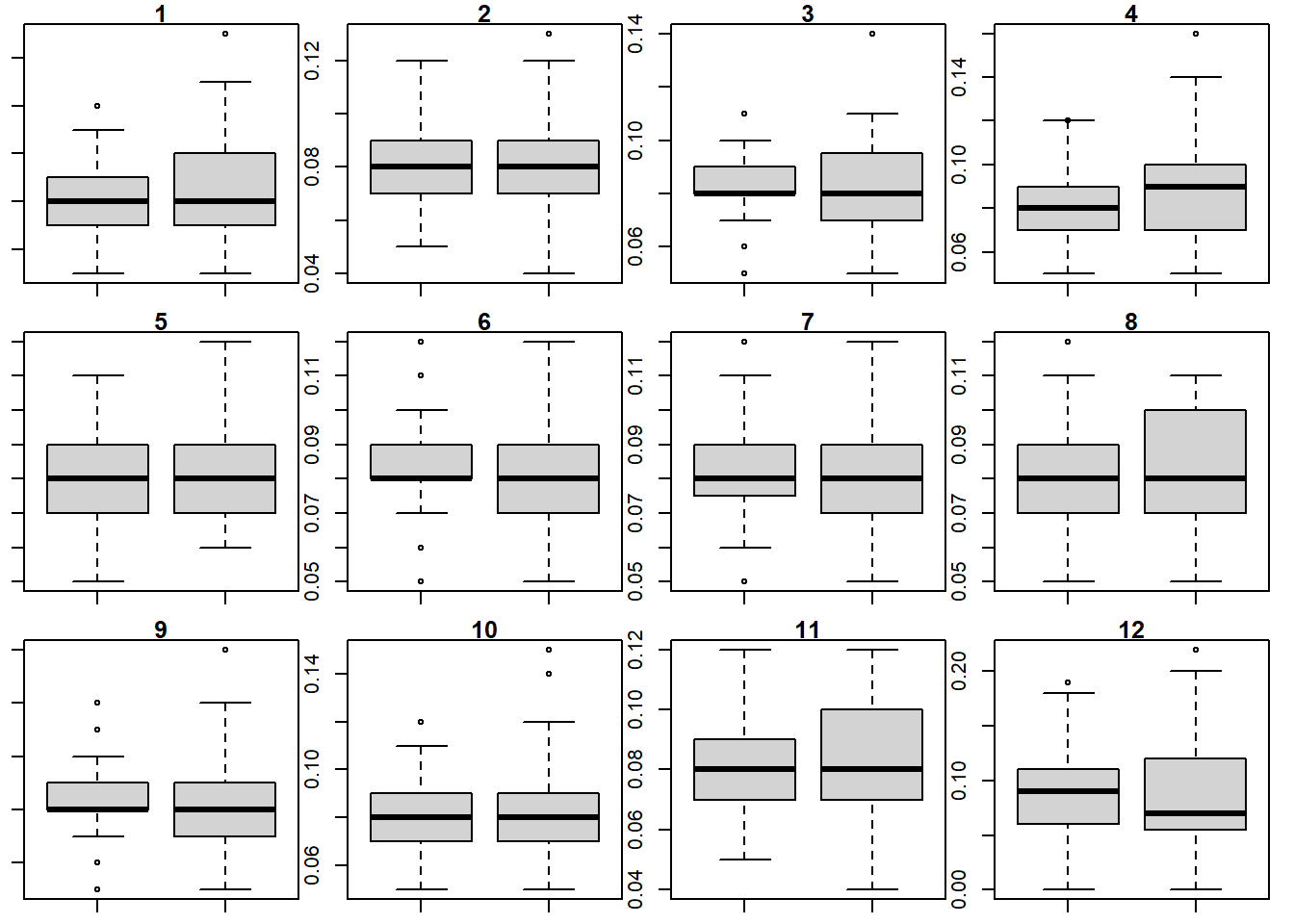

IC <- which(IC)
OC <- which(OC)
col <- c(rep(1, length(IC)), rep(2, length(OC)))
matplot(ora, t(R[c(IC,OC),-1]), type="l", col=col)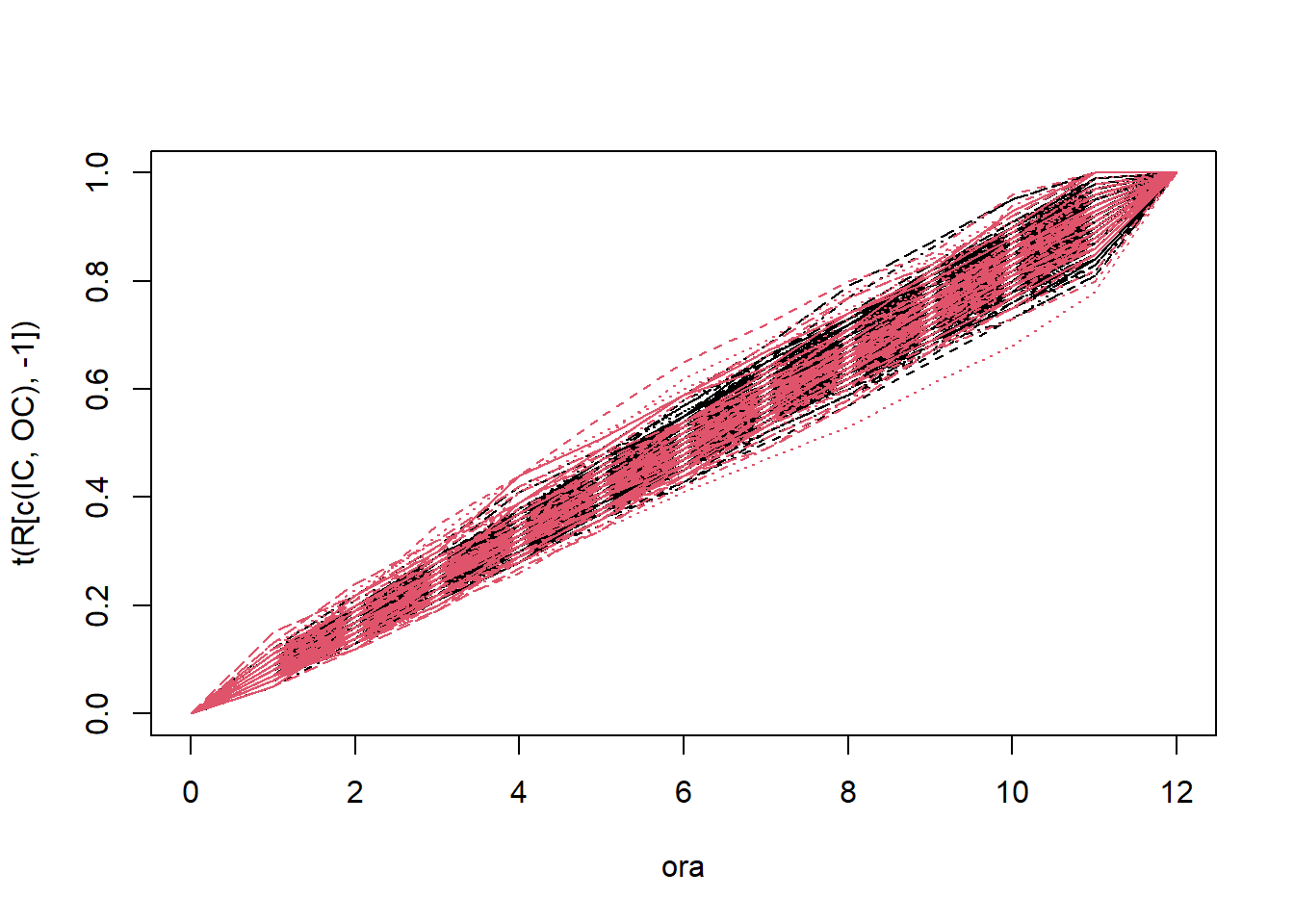

Il problema sembra essere solamente di aumentata variabilità (o almeno così dice il Masarots, a me non pare). L’azienda ha rilevato che tra il lotto 42 e 66 la richiesta di farmaci era aumentata, il ché potrebbe aver portato a una minore regolarità nel deposito della sostanza (l’applicazione della membrana è avvenuta per gruppi più numerosi contemporaneamente).

Caso 5: I semiconduttori devono essere cotti a puntino!

Nella produzione di semiconduttori, i wafer di silicio sono rivestiti con una sostanza che dopo essere stata applicata viene cucinata in un forno a temperature relativamente alte in maniera che si espanda e aderisca meglio. Per ogni infornata vengono misurati 5 wafer. flow1 contiene 25 lotti su cui è stata costruita una carta di Shewhart per la media, mentre flow2 contiene le misurazioni per altri 20 lotti successivi (sempre 5 misurazioni per lotto).

x1 <- scan("~/Uni/Controllo/Datasets/flow1")
x2 <- scan("~/Uni/Controllo/Datasets/flow2")
str(x1)
 num [1:125] 1.32 1.41 1.67 1.46 1.69 ...
str(x2)
 num [1:100] 1.45 1.55 1.45 1.43 1.62 ...
n <- 5; m <- 25
d1 <- matrix(x1, n, m)
Ls <- shewhart.normal.limits(n=n, m=m, stat="S")
shewhart(d1, stat="S", limits=Ls)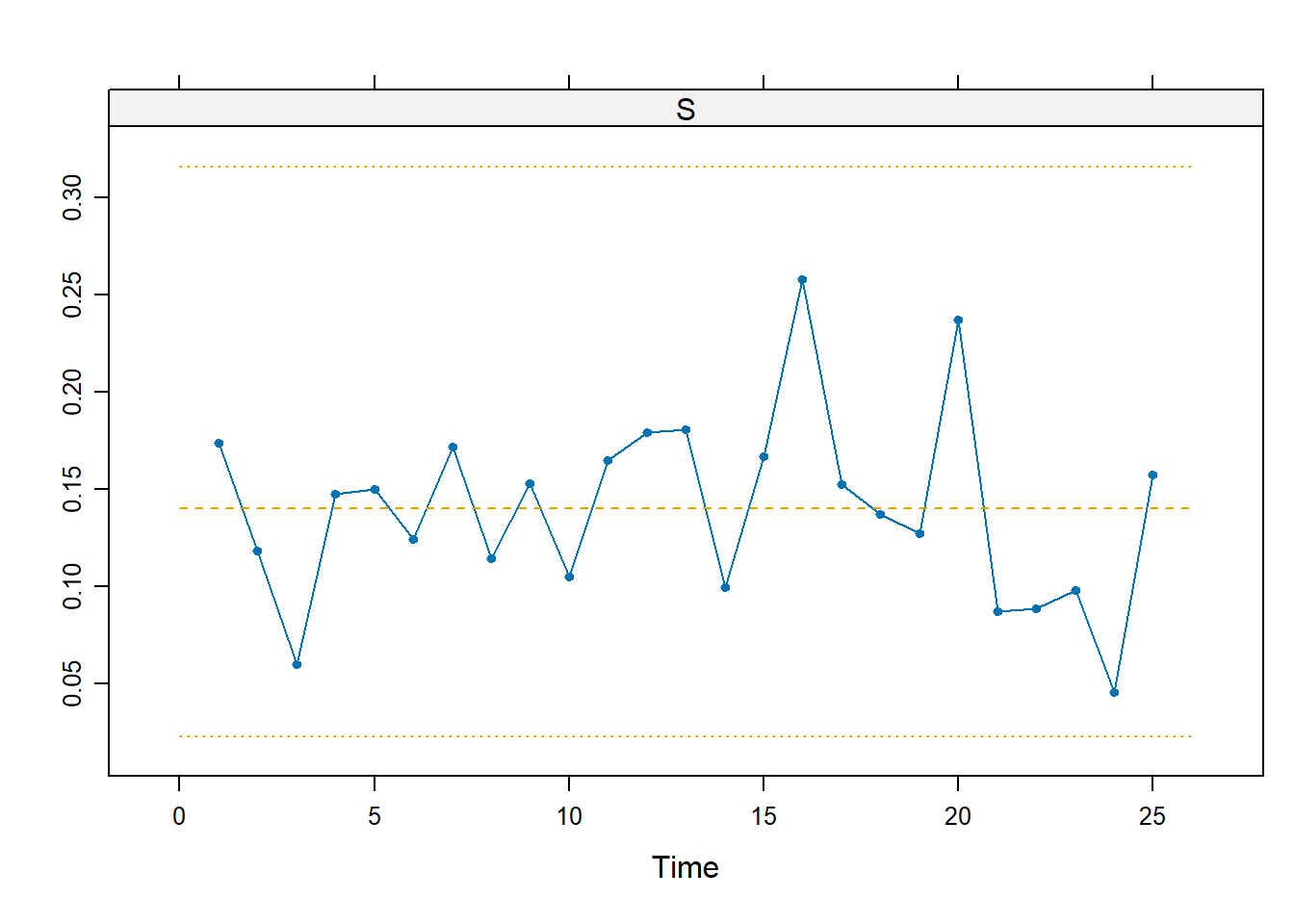

Lx <- shewhart.normal.limits(n=n, m=m, stat="Xbar")
shewhart(d1, stat="Xbar", limits=Lx)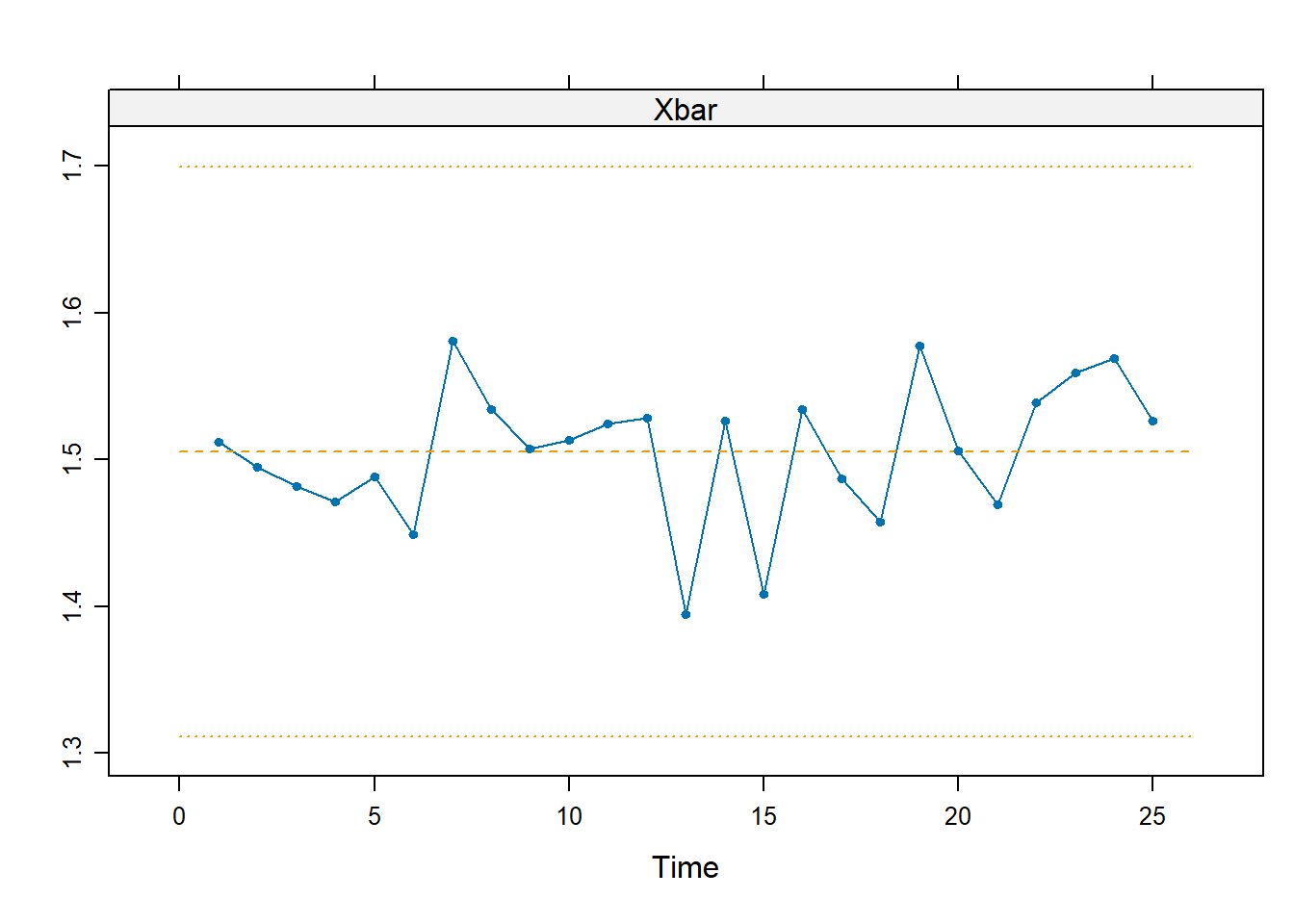

rsp(d1)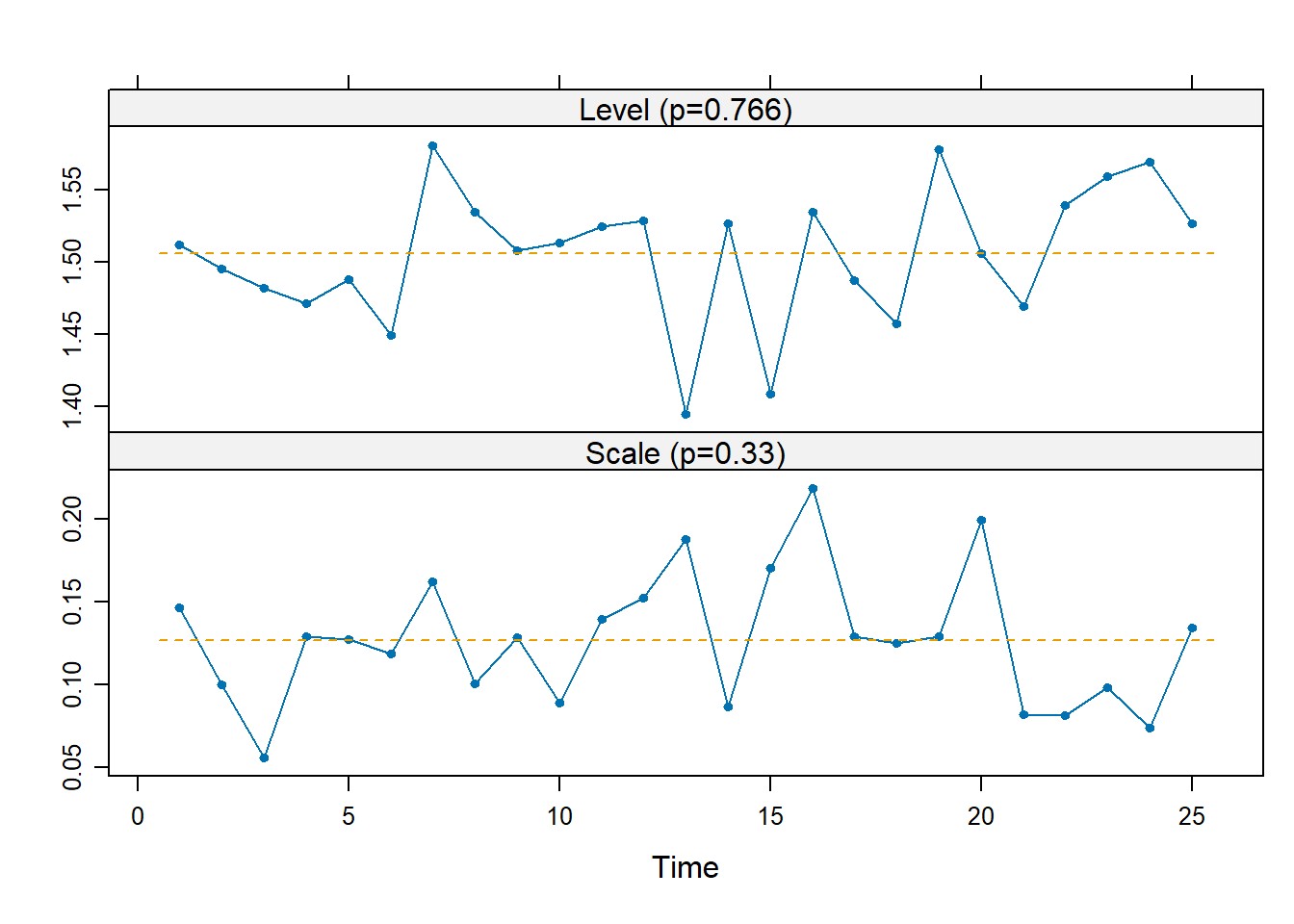

Non emergono allarmi nè irregolarità. Il test di Shapiro-Wilk non dà indicazioni contro la normalità (anzi, \(p=0.97\)).

Questi dati possono allora essere utilizzati per stimare i valori del processo in controllo

mu0 <- mean(x1)
sigma0 <- sd(x1)
c(mu0=mu0, sigma0=sigma0)
      mu0    sigma0 
1.5056104 0.1332335

Carte di controllo per la fase II

Vogliamo costruire le carte di controllo per media e varianza in modo che \(ARL \simeq 2000\)

Per la media:

B <- 2000
se0 <- sigma0/sqrt(n)
LCLx <- qnorm(1/(2*B), mu0, se0)
UCLx <- qnorm(1-1/(2*B), mu0, se0)
c(se=se0, LCLx=LCLx, UCLx=UCLx)
        se       LCLx       UCLx 
0.05958385 1.29821354 1.71300726

Per la varianza (unilaterale):

LCLs <- 0
UCLs <- sigma0*sqrt(qchisq(1-1/B, n-1)/(n-1))
c4 <- sqrt(2/(n-1))*gamma(n/2)/gamma((n-1)/2)
CLs <- c4*sigma0
c(LCLs=LCLs, CLs=CLs, UCLs=UCLs)
     LCLs       CLs      UCLs 
0.0000000 0.1252376 0.2978995 
d2 <- matrix(x2, n)
xbar <- colMeans(d2)
s <- apply(d2, 2, sd)
matplot(cbind(xbar, mu0, LCLx, UCLx), 
        type=c("b","l","l","l"), 
        lty=c("solid", "dotted", "dashed", "dashed"),
        lwd=3, pch=1, col=c(4, "gray", "gray", "gray"),
        xlab="t", ylab=expression(bar(x)[t]))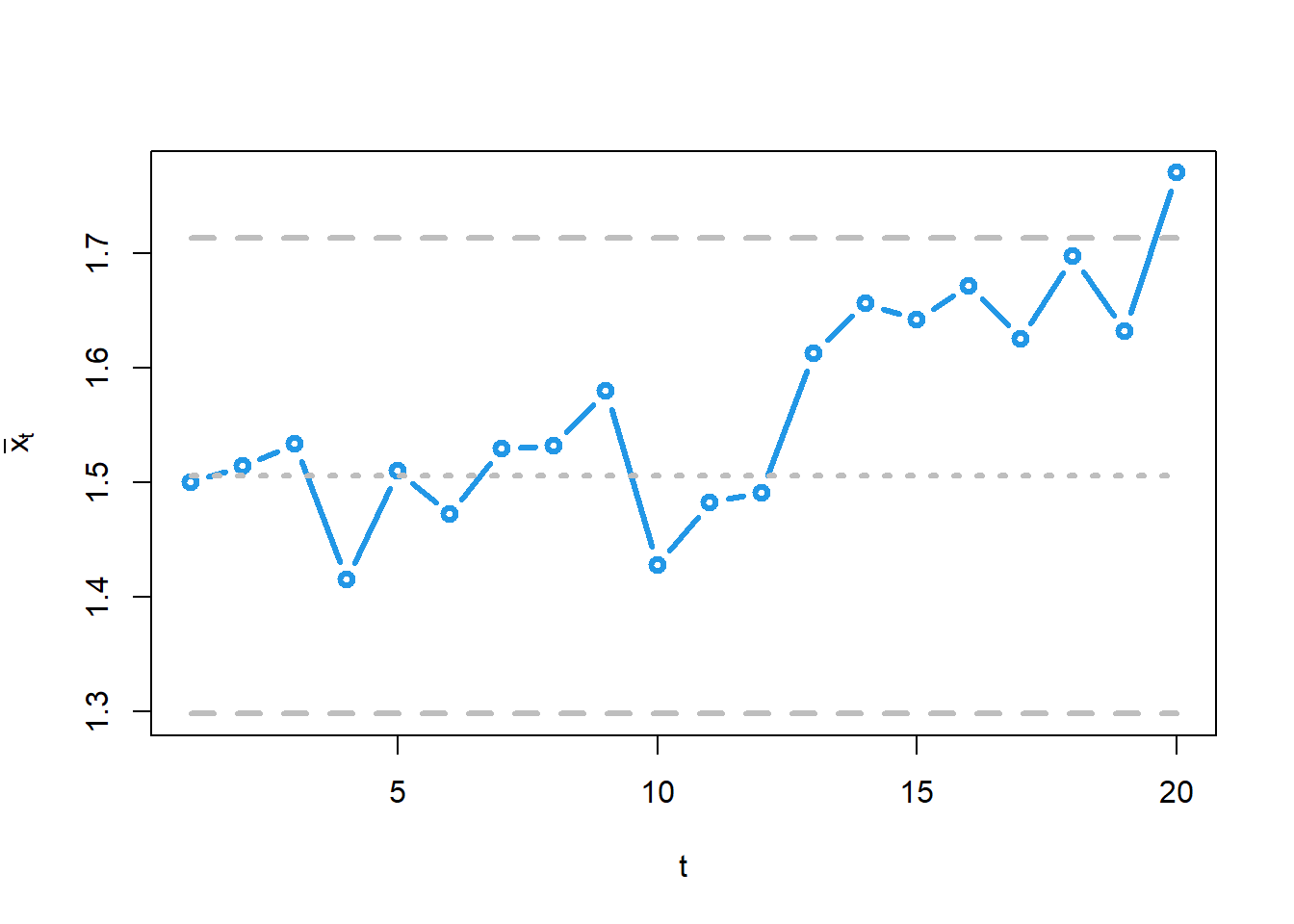

matplot(cbind(s, CLs, LCLs, UCLs),
        type=c("b","l","l","l"),
        lty=c("solid", "dotted", "dashed", "dashed"),
        lwd=3, pch=1, col=c(4, "gray", "gray", "gray"),
        xlab="t", ylab=expression(S[t]))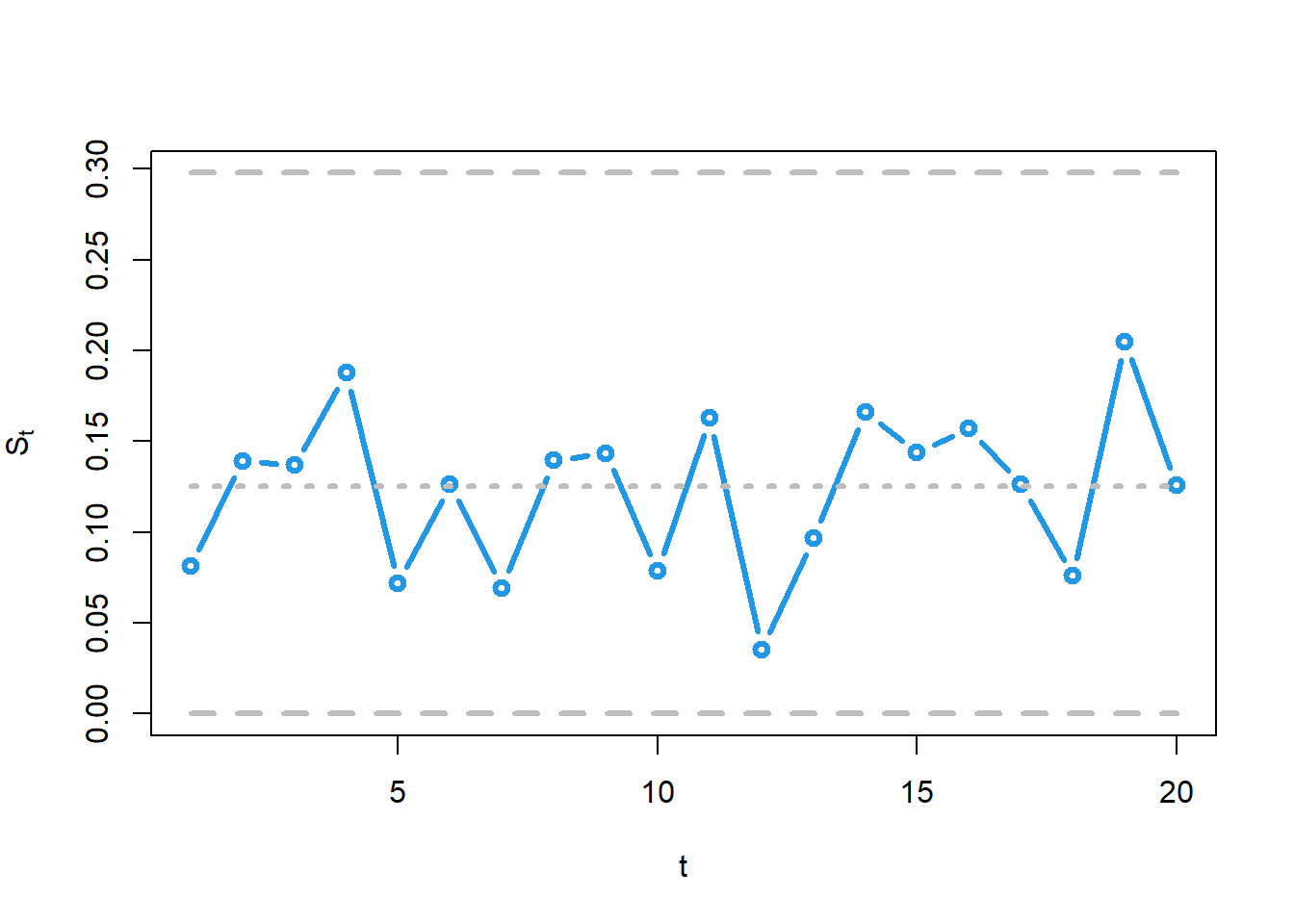

Si noti che i dati in flow2 sono in realtà raccolti sequenzialmente, dunque questi grafici sono in realtà disegnati progressivamente, da sx a dx, dopo le misurazioni di ogni singolo lotto.

Viene segnalato un allarme per la media nell’ultima osservazione. In effetti, dalla 12esima le medie sembrano essere particolarmente alte, seppur entro i limiti, ad indicare che potrebbe essere successo qualcosa.

Per calcolare l’ARL fuori controllo della carta per la media, si ha \[ E[RL] = \frac{1}{\theta_1} \] dove \(\theta_1= Pr (Wt < LCL \text{ oppure } Wt > UCL)\) è la probabilità di cadere fuori dai limiti di controllo. Si ricordi che per le carte di Shewhart l’ARL fuori controllo e l’EDD coincidono.

salto <- c(0.1, 0.2, 0.3)
arl1 <- 1 / (pnorm(LCLx, mu0 + salto, se0) + pnorm(UCLx, mu0 + salto, se0, lower.tail = FALSE))
names(arl1) <- salto
arl1
      0.1       0.2       0.3 
27.981812  2.219256  1.063912

Inoltre possiamo anche disegnare l’intera distribuzione dell’ARL fuori controllo

x <- 1:100
par(mfrow=c(1,3))
plot(x, (1/arl1[1])*(1-1/arl1[1])^(x-1), type="h",
     main=salto[1], xlab="", ylab="")
plot(x, (1/arl1[2])*(1-1/arl1[2])^(x-1), type="h",
     main=salto[2], xlab="", ylab="")
plot(x, (1/arl1[3])*(1-1/arl1[3])^(x-1), type="h",
     main=salto[3], xlab="", ylab="")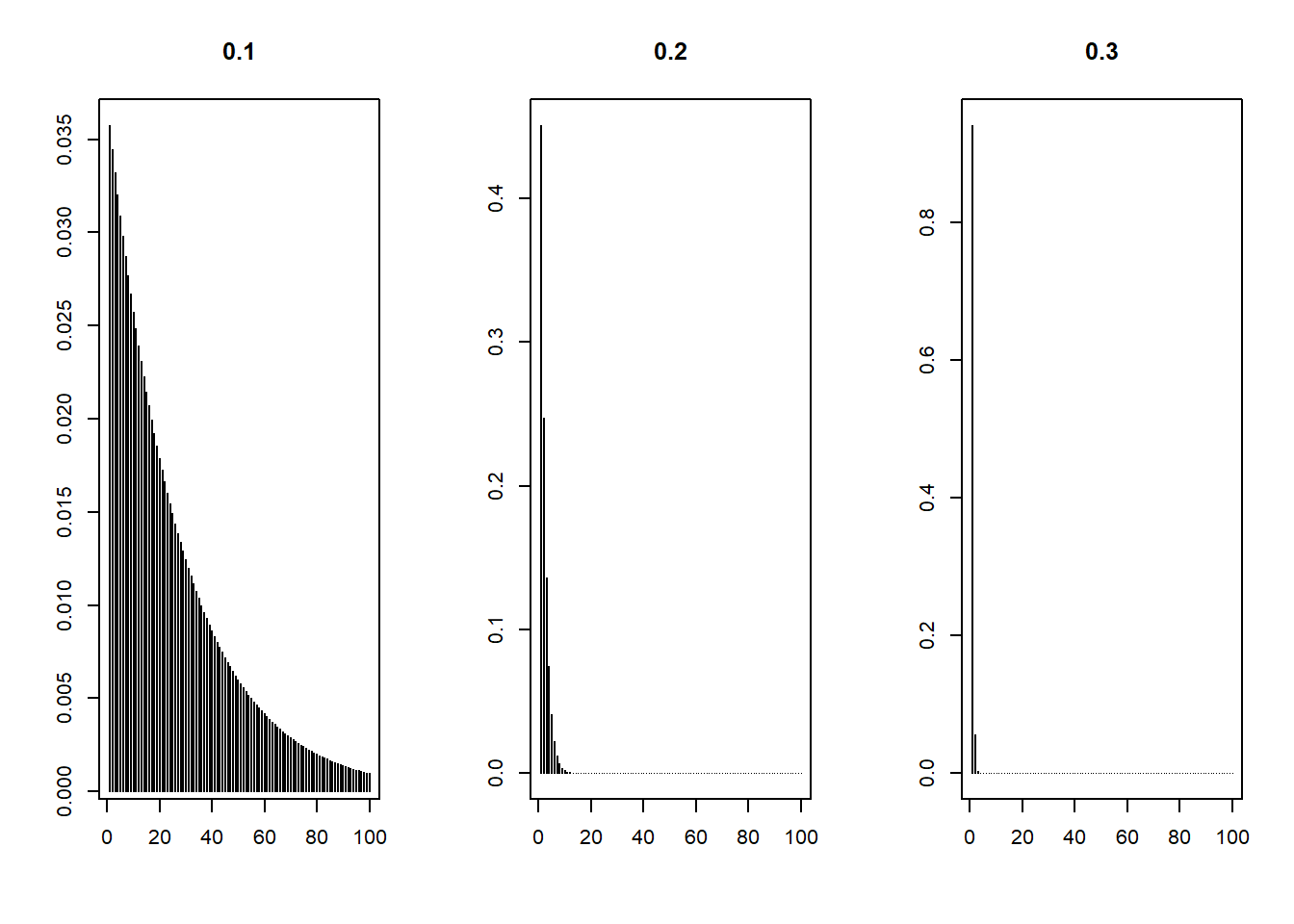

par(mfrow=c(1,1))

Per la carta della varianza

omega <- c(1.2, 1.5, 2)
arl1 <- 1/(1-pchisq(qchisq(1-1/B, 3)/omega^2, 3))  # non ho capito perché 3 df
names(arl1) <- omega
arl1
       1.2        1.5          2 
156.596000  20.593934   4.578947

Si possono disegnare analogamente le distribuzioni (tralasciamo).

Caso 6: Sui melanomi tra le donne a New York

I dati indicano il numero di donne malate di melanoma e il numero di donne residenti a New York negli anni tra il 1976 e il 2010.

d <- read.table("~/Uni/Controllo/Datasets/manhattan", header=TRUE)
str(d)
'data.frame':   35 obs. of  3 variables:
 $ year      : int  1976 1977 1978 1979 1980 1981 1982 1983 1984 1985 ...
 $ cases     : int  55 42 51 47 53 52 52 46 63 33 ...
 $ population: num  8.73 9.13 7.85 8.39 8.41 8.25 8.67 8.68 8.87 8.25 ...
plot(ts(cbind(Casi=d$cases, Popolazione=d$population, Incidenza=d$cases/d$population),
        start=d$year[1]), main="", xlab="Anni")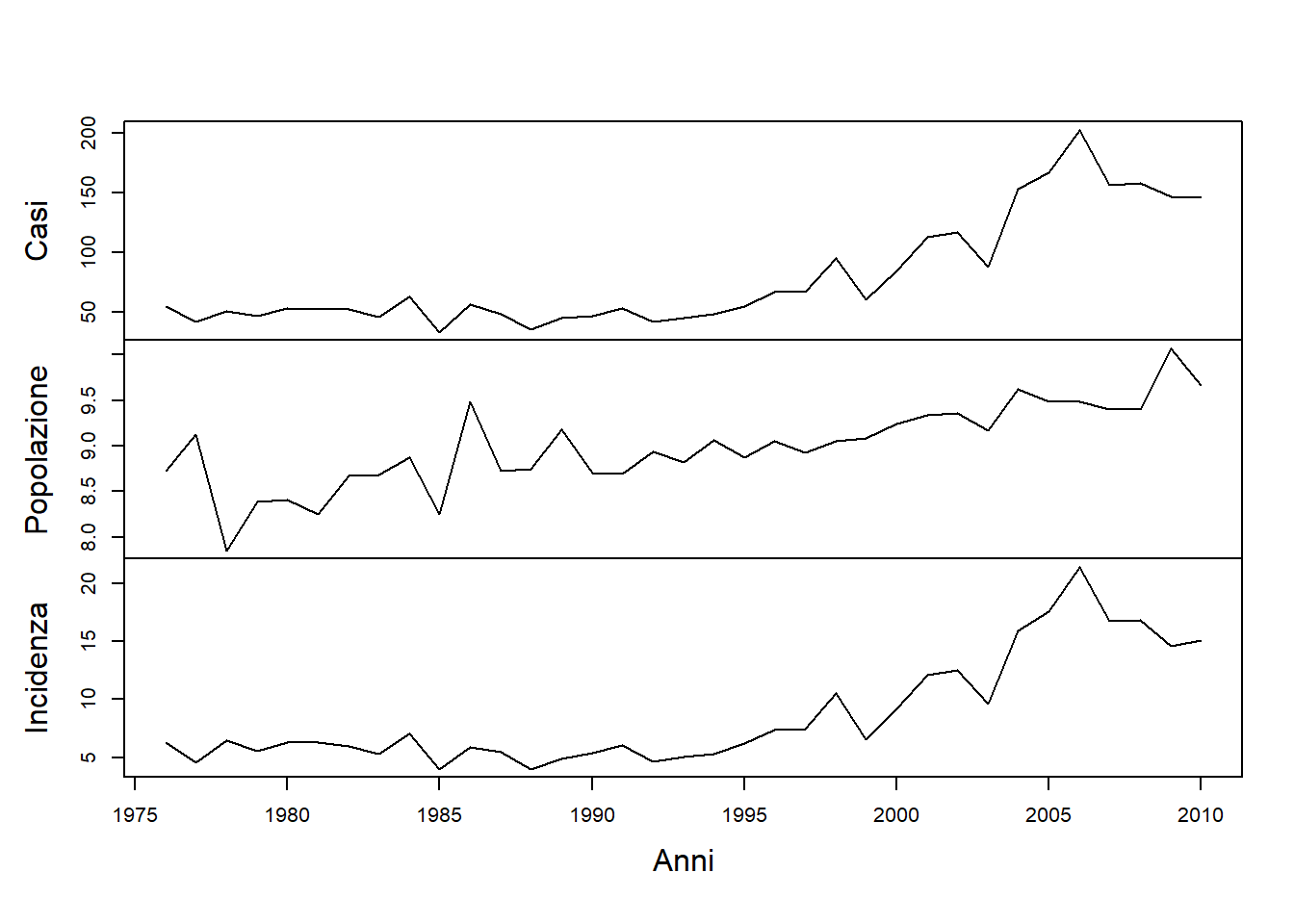

Assumiamo \[ x_t \sim Po(u_t, n_t) \] con \[ u_t = \begin{cases} u_0, & t \le 1995,\\ u_t > u_0, & t > 1995. \end{cases} \]

Immaginiamo di essere a inizio 1986. Stimiamo il valore in controllo \(\hat{u}_0\) con

u0 <- sum(d$cases[1:10])/sum(d$population[1:10])
u0
[1] 5.796081

Ci aspettiamo circa 6 casi ogni 100.000 donne. Nel 1985, la distribuzione dei casi stimata era

m <- u0*d$population[10]
casi <- 0:qpois(1-1/10^9, m)
plot(casi, dpois(casi, m), type="h", xlab="casi", ylab="probabilità")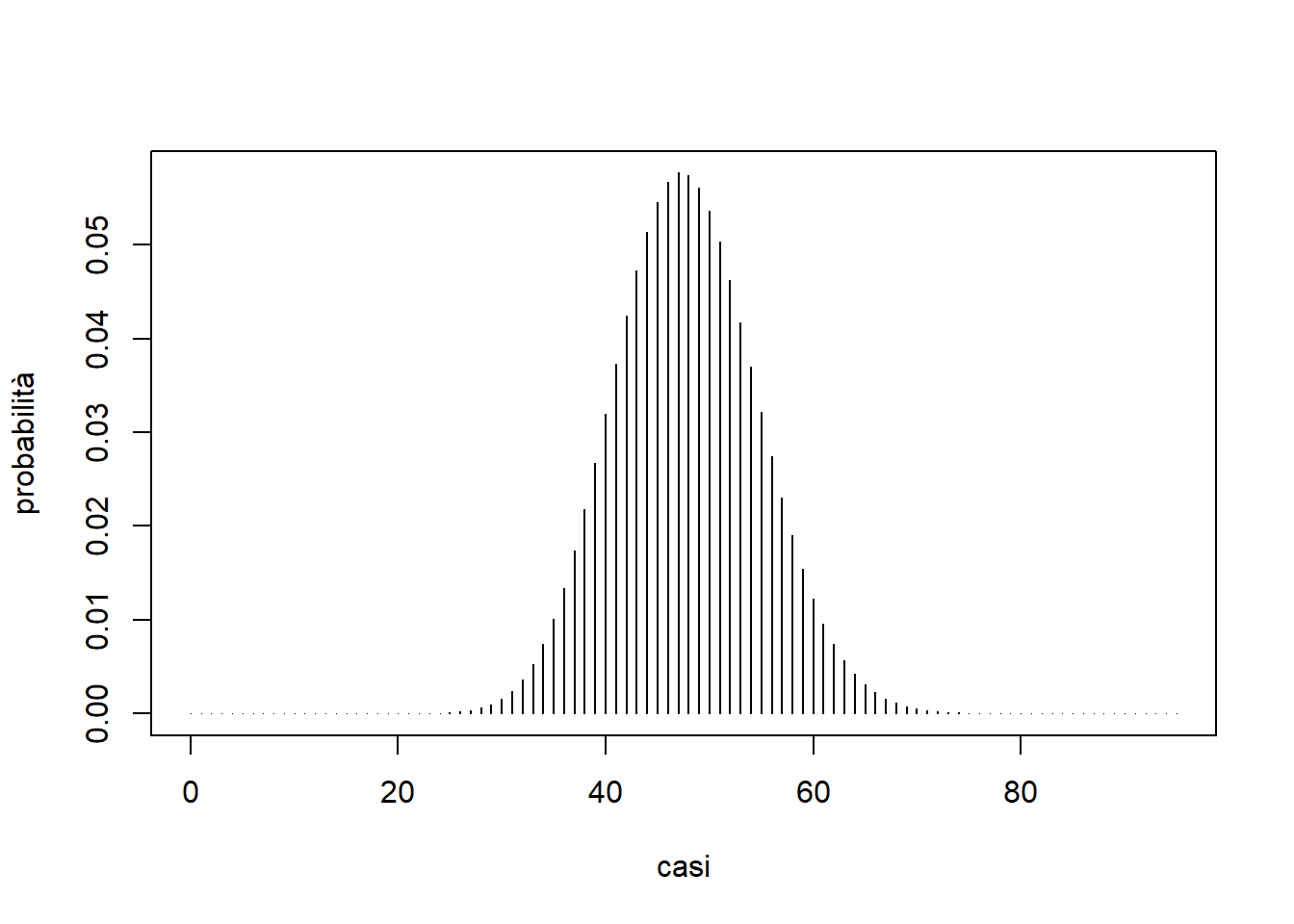

Usiamo \(W_t=x_t\) e non \(W_t=\frac{x_t}{n_t}\) per tradizione epidemiologica (le due opzioni sono equivalenti nel senso che segnalerebbero sempre gli stessi allarmi).

Siamo interessati a un controllo unilaterale. Se vogliamo ARL pari a 10

B <- 10
a <- NULL
for (i in 11:NROW(d)) {
  anno <- d$year[i] # anno corrente
  xt <- d$cases[i] # casi osservati
  cl <- u0*d$population[i] # casi attesi (center line)
  UCL <- qpois(1-1/B, cl) # limite superiore
  a <- rbind(a, c(anno, xt, cl, UCL)) # matrice x il grafico
  decisione <- if (xt<=UCL) "OK" else "ALLARME"
  if (decisione=="ALLARME") break
}
matplot(a[,1], a[,-1], type=c("b","l","l"), 
        lty=c("solid", "dotted", "dashed"),
        lwd=3, pch=1, col=c(4, "gray", "gray"),
        xlab="anno", ylab="casi di melanoma")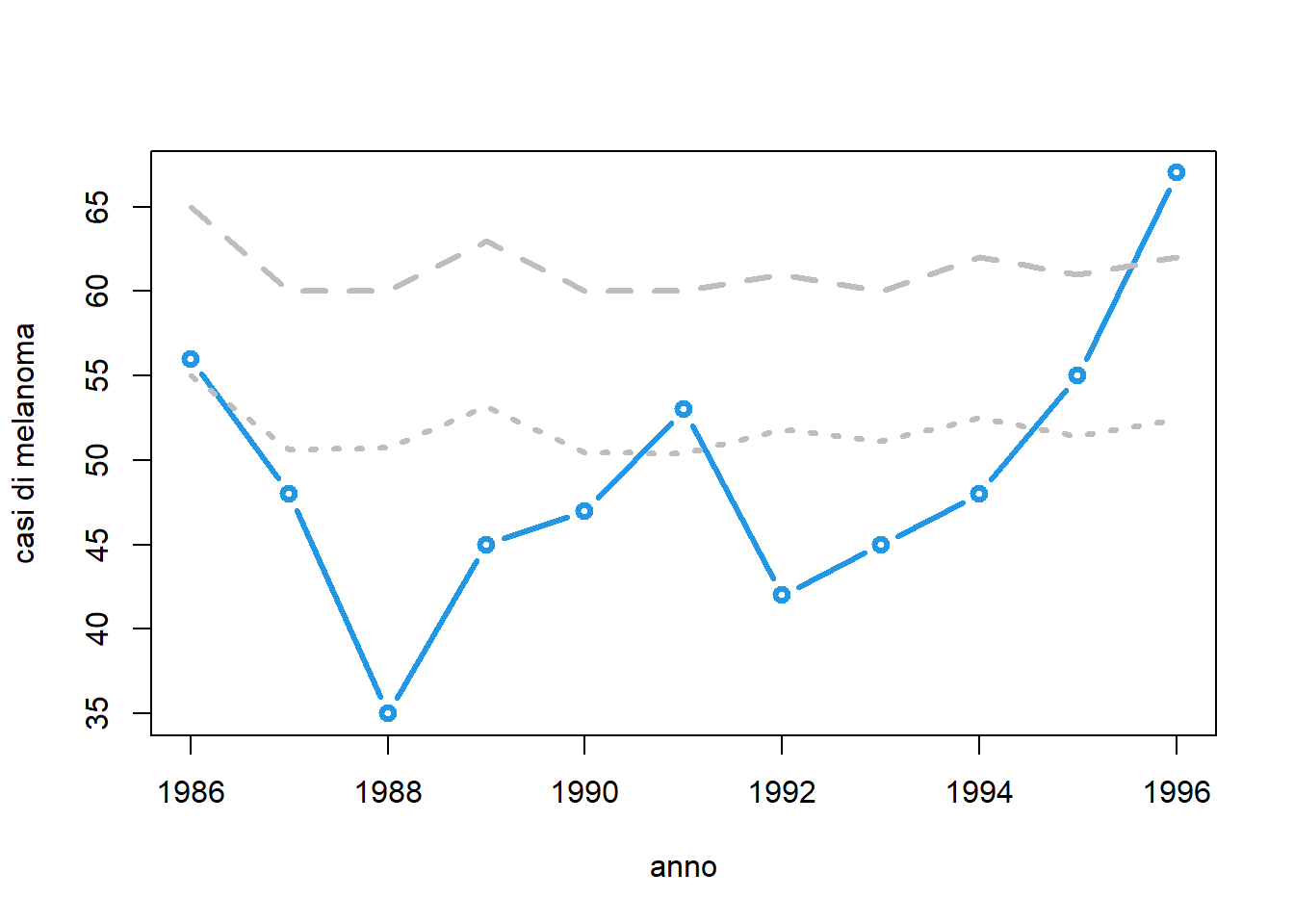

Se ci sentiamo un po’ pazzerelli potremmo vedere cosa succede accettando un falso allarme ogni milione di anni

  B <- 1000000
  a <- NULL
  for (i in 11:NROW(d)) {
  anno <- d$year[i] # anno corrente
  xt <- d$cases[i] # casi osservati
  cl <- u0*d$population[i] # casi attesi (center line)
  UCL <- qpois(1-1/B, cl) # limite superiore
  a <- rbind(a, c(anno, xt, cl, UCL)) # matrice x il grafico
  decisione <- if (xt<=UCL) "OK" else "ALLARME"
  if (decisione=="ALLARME") break
  }

matplot(a[,1], a[,-1],
  type=c("b","l","l"),
  lty=c("solid", "dotted", "dashed"),
  lwd=3, pch=1,
  col=c(4, "gray", "gray"),
  xlab="anno", ylab="casi di melanoma")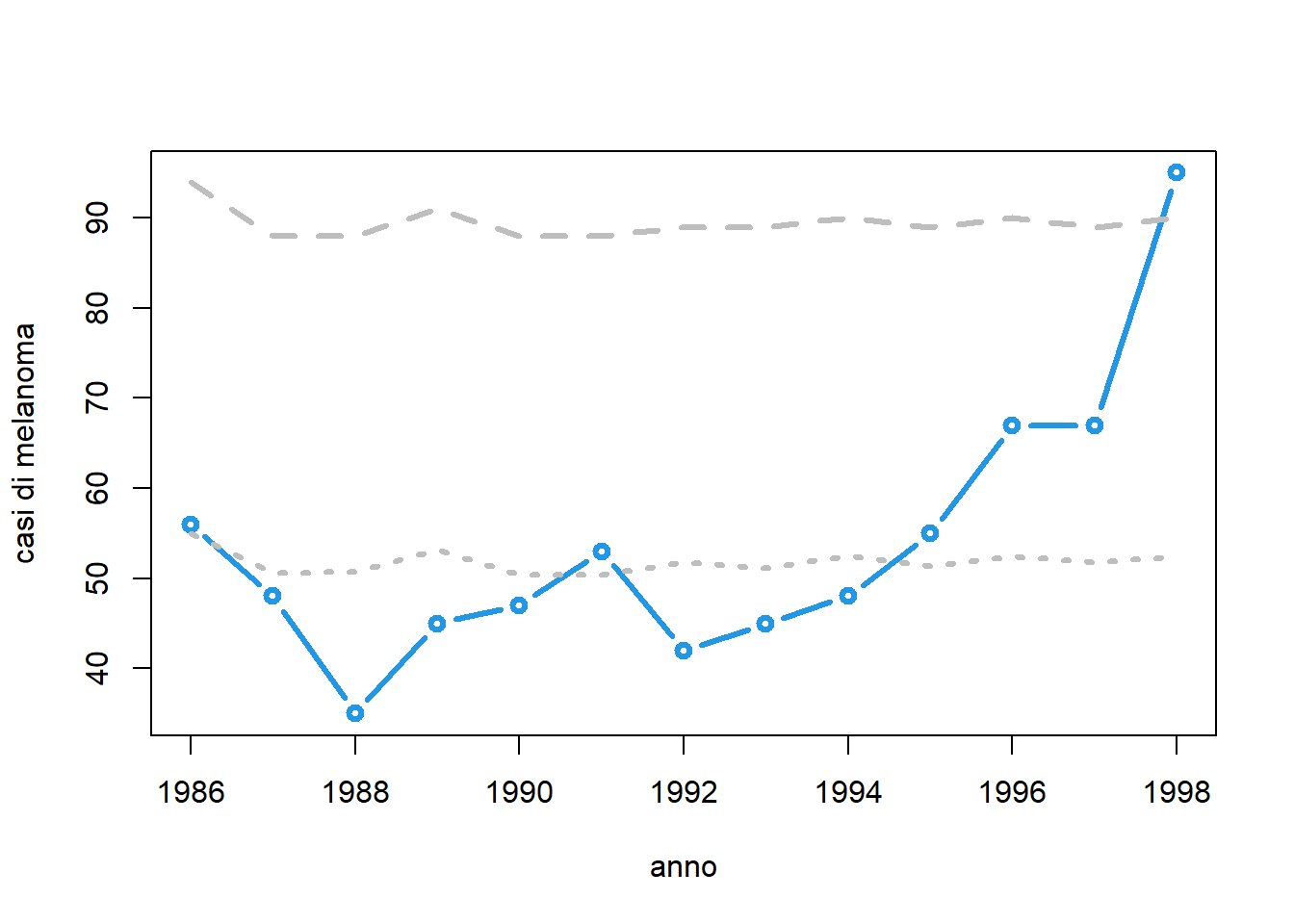

Anche in questo caso segnaleremmo un allarme, ma due anni più tardi. Questo significa che il cambio nella distribuzione è certamente presente. La scelta dell’ARL risente dell’usuale trade-off tra FAP e EDD.

Caso 7: Ogni quanto tempo fare quante misure è un problema degli statistici!

Una azienda produce 24 ore su 24 una sostanza chimica fluida, di cui va monitorata la viscosità. Questa ha distribuzione normale di media e varianza assunte note. Si vuole utilizzare una carta di Shewhart per la media. Il problema è scegliere un appropriato schema di campionamento, sapendo che l’azienda non è disposta a raccogliere più di 24 campioni al giorno. Pertanto le opzioni possibili sono 1 campione all’ora, 2 campioni ogni 2 ore, …, 12 ogni 12 ore. Non vi sono motivi esterni che rendano un disegno preferibile all’altro, dunque va determinato quale sia più efficiente.

Si consideri ARL accettabile pari a 30 giorni e necessità di rilevare velocemente salti di modulo maggiore di \(2 \sigma_0\).

La soluzione naturale è considerare l’Average Time to Signal (ATS) invece dell’EDD che qui perderebbe di significato pratico. Per un processo che campiona ogni \(H\) ore, si ha che \[ ATS = \frac{H}{2} + (EDD - 1) H \] che, pensandoci, ha senso, considerando che in media il primo campionamento fuori controllo avviene \(\frac{H}{2}\) ore dopo il guasto.

delta <- 2  # dimensione salto da identificare rapidamente
H <- 1:12
se0 <- 1/sqrt(H)  # standard error delle medie
B <- 30*24/H
## Limiti
LCL <- qnorm(1/(2*B), 0, se0)
UCL <- qnorm(1-1/(2*B), 0, se0)
## ARL (numero medio di campioni prima di un allarme)
ARL0 <- 1/(pnorm(LCL, 0, se0)+pnorm(UCL, 0, se0, lower.tail = FALSE))  # IC
ARL1 <- 1/(pnorm(LCL,delta, se0)+ pnorm(UCL, delta, se0, lower.tail = FALSE))  # OC (salto=2sigma)
## ATS: Average Time before Signal (in ore)
ATS0 <- H*ARL0  # IC
ATS1 <- H/2+(ARL1-1)*H  # OC
plot(H, ATS1, type="h",
     xlab="frequenza di campionamento (ore)", ylab="ritardo atteso (ore)")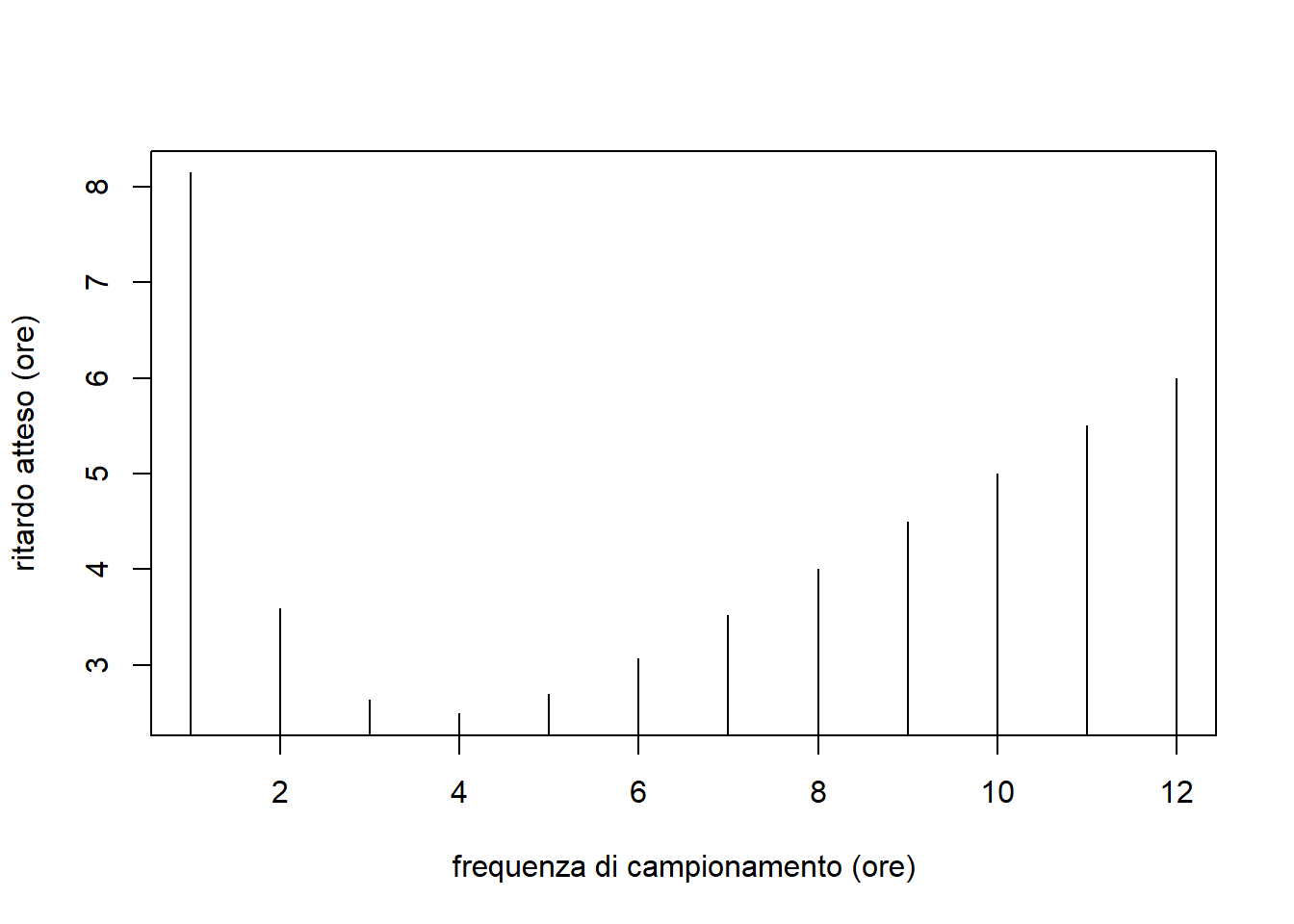

Lo schema più efficiente per salti di \(\pm 2 \sigma_0\)è quello che raccoglie 4 osservazioni ogni 4 ore.

Caso 8: Sul perchè, dopo qualche tempo, si è deciso di controllare la bontà delle ‘infornate’ di semiconduttori con delle carte di controllo di tipo CuSum

I dati sono quelli del Caso 5. L’azienda si è accorta che il processo è frequentemente soggetto a instabilità della varianza e la carta di Shewhart le segnala troppo lentamente. Per questo motivo si è deciso di passare a una carta CuSum. Vogliamo rilevare salti nella media di \(\pm 0.2\) micron e aumenti della std del 50%, mantenendo ARL 2000.

Risulta

mu0 <- mean(x1)
sigma0 <- sd(x1)
c(mu0=mu0, sigma0=sigma0)
      mu0    sigma0 
1.5056104 0.1332335 
n <- 5
delta <- 0.2/sigma0
kx <- sqrt(n)*delta/2  # valore di riferimento k
kx
[1] 1.678307
B <- 2000
library(spc)
Lx <- xcusum.crit(kx, B, sided="two")  # valore critico L
Lx
       h 
1.908576

Le ARL fuori controllo comparate risultano

# per CuSum
ARL01 <- xcusum.arl(kx, Lx, mu=sqrt(n)*salto[1]/sigma0, sided="two")
ARL02 <- xcusum.arl(kx, Lx, mu=sqrt(n)*salto[2]/sigma0, sided="two")
ARL03 <- xcusum.arl(kx, Lx, mu=sqrt(n)*salto[3]/sigma0, sided="two")
c(ARL01, ARL02, ARL03)
[1] 9.430442 1.762996 1.074104
# per Shewhart
se0 <- sigma0/sqrt(n)
LCLs <- qnorm(1 / (2 * B), mu0, se0)
UCLs <- qnorm(1 - 1 / (2 * B), mu0, se0)
1 / (pnorm(LCLs, mu0 + salto, se0) +
pnorm(UCLs, mu0 + salto, se0, lower.tail = FALSE)
)
[1] 27.981812  2.219256  1.063912

Si veda il CuSum per la varianza…

Caso 9: The use of a CUSUM residual chart to monitor respiratory syndromic data (grazie Gemini)

Questo studio affronta il monitoraggio di dati sulla salute pubblica (conteggi giornalieri di visite per sindrome respiratoria) per rilevare precocemente epidemie. Tali dati non sono stabili né indipendenti, ma mostrano stagionalità, effetti di calendario (giorni feriali, festivi come il Capodanno Cinese), trend e autocorrelazione.

La strategia di Controllo Statistico della Qualità (SQC) adottata è il monitoraggio dei residui, articolata in due fasi:

  1. Fase I: Modellazione del Processo (Definizione della Baseline “In Controllo”) L’obiettivo è filtrare tutta la variabilità prevedibile dai dati grezzi. I dati del 2005-2006 sono usati per:
    • Trasformare i conteggi giornalieri (Yt) con una trasformazione di Box-Cox (λ=0.96) per ottenere Wt.
    • Modellare Wt con una regressione che include variabili dummy per giorno della settimana, mese, festività specifiche, effetti tifone, funzioni sinusoidali per la stagionalità annuale e un trend lineare, oltre a termini di interazione.
    • Modellare il termine d’errore (εt) della regressione con un modello ARIMA (complesso, con p=8 e q fino a 30) per catturare l’autocorrelazione residua. I residui finali di questo modello (at, indicati come Rt nel paper) sono considerati rumore bianco con deviazione standard stimata σR ≈ 83.4.
  2. Fase II: Monitoraggio del Processo (Rilevamento Segnali “Fuori Controllo”) Per rilevare aumenti anomali (potenziali epidemie), si utilizza una carta CUSUM (CUmulative SUM) unilaterale superiore sui residui standardizzati Rt/σR.
    • Statistica CUSUM: Ct+ = max(0, Rt/σR - k + Ct-1+)
    • Parametri: k = 0.5 (per rilevare uno shift di 1σR), C0+ = 0.
    • Limite di Controllo: h = 2.225, scelto per ottenere una Lunghezza Media di Sequenza (ARL0) in controllo di 50. Un allarme scatta se Ct+ > h.

Il modello, stimato sui dati 2005-2006, è stato poi validato monitorando i dati del 2007-2008, mostrando la capacità della carta CUSUM di segnalare periodi di attività anomala.

In sintesi, lo studio dimostra come adattare i principi SQC a dati complessi, modellando accuratamente la baseline per poi monitorare le deviazioni significative da essa tramite una carta CUSUM sui residui.

Questo codice mostra come calcolare la statistica CUSUM (Ct+) assumendo di avere già i residui standardizzati z_t = R_t/σ_R.

# Parametri per la carta CUSUM come nel paper
k_param <- 0.5  # Valore di riferimento (k)
h_param <- 2.225 # Limite di controllo (h)

# Simuliamo dei residui standardizzati (z_t = R_t/sigma_R)
# Questi sarebbero l'output della complessa Fase I di modellazione
set.seed(123)
n_in_controllo <- 100      # Osservazioni in controllo
n_fuori_controllo <- 50     # Osservazioni fuori controllo (con uno shift)
shift_std <- 1.0           # Ampiezza dello shift (delta = 1 sigma_R)

residui_std_in_controllo <- rnorm(n_in_controllo, mean = 0, sd = 1)
residui_std_fuori_controllo <- rnorm(n_fuori_controllo, mean = shift_std, sd = 1)
residui_std_totali <- c(residui_std_in_controllo, residui_std_fuori_controllo)
tempo <- 1:length(residui_std_totali)

# Calcolo manuale della CUSUM unilaterale superiore (C_t+)
C_piu <- numeric(length(residui_std_totali))
C_piu[1] <- max(0, residui_std_totali[1] - k_param) # Assumendo C_0_piu = 0

for (t in 2:length(residui_std_totali)) {
  C_piu[t] <- max(0, residui_std_totali[t] - k_param + C_piu[t-1])
}

# Grafico della CUSUM
plot(tempo, C_piu, type = 'l', col = 'blue',
     xlab = "Tempo (t)", ylab = "C_t+",
     main = "CUSUM Unilaterale Superiore su Residui Standardizzati")
abline(h = h_param, col = "red", lty = 2) # Limite di controllo h
abline(v = n_in_controllo + 0.5, col = "darkgreen", lty = 3, lwd = 1.5) # Inizio dello shift
legend("topleft", legend = c("C_t+", paste("Limite h =", h_param), "Inizio Shift"),
       col = c("blue", "red", "darkgreen"), lty = c(1, 2, 3), lwd=c(1,1,1.5))

# Identifica i punti di allarme
punti_allarme <- tempo[C_piu > h_param]
if(length(punti_allarme) > 0) {
  points(punti_allarme, C_piu[punti_allarme], col = "red", pch = 19)
  cat("Allarmi generati ai tempi:", punti_allarme, "\n")
} else {
  cat("Nessun allarme generato con questi dati simulati.\n")
}

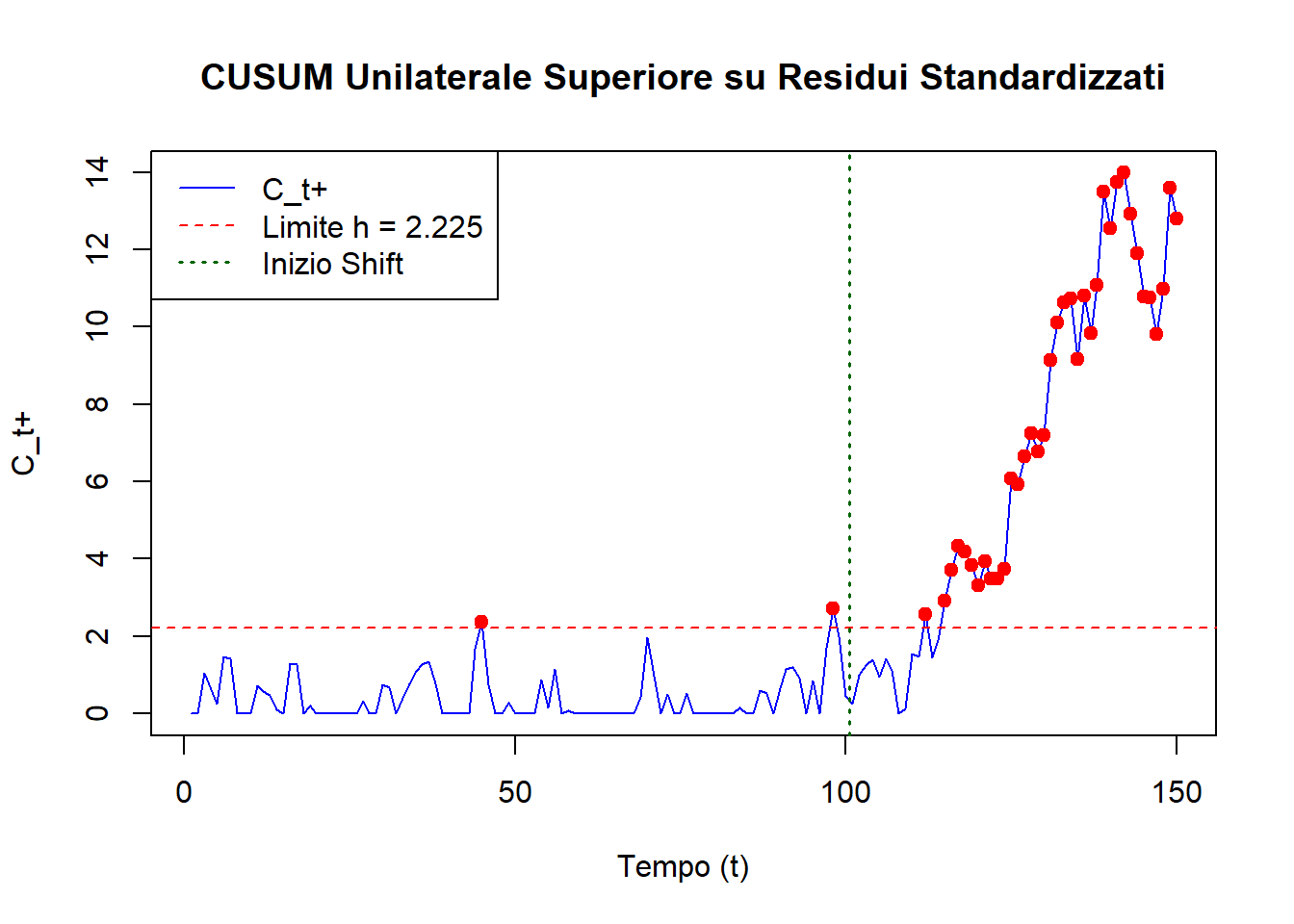
Allarmi generati ai tempi: 45 98 112 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150

Caso 10: Ancora su di un broncodilatatore a rilascio lento

I dati sono quelli del Caso 4. Dopo il 32esimo lotto vogliamo cominciare ad effettuare una sorveglianza di Fase II. Vogliamo ARL in controllo di 10 anni e rilevare variazioni della media di \(\pm 0.005\) con EDD inferiore a 10, di \(\pm 0.02\) con EDD inferiore a 1.5.

Verifichiamo che nelle prime 32 osservazioni, di Fase I, la media fosse effettivamente stabile, in modo da poterne ottenere una stima. Utilizzando RS/P si ha

D <- R[, 3:14] - R[, 2:13]  # rilasci orari
u <- apply(D[, 1:10], 1, max)
d1 <- matrix(u[R$lotto <= 32], 5)
d2 <- matrix(u[R$lotto > 32], 5)
dfphase1::rsp(d1)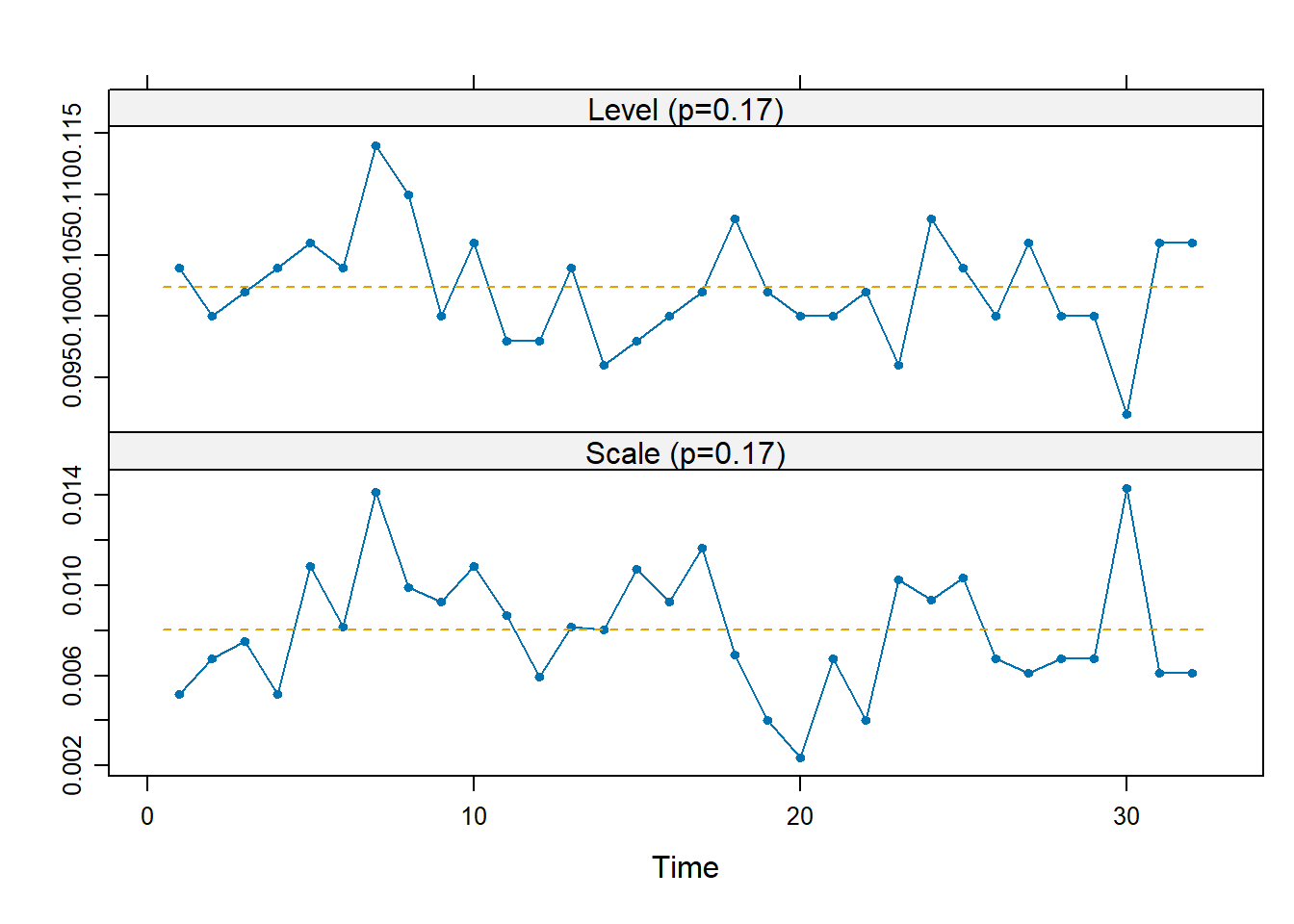

Su tutti i dati raccolti la normalità è inverosimile. Tuttavia, questa diventa un’ipotesi plausibile sulle medie dei gruppi, come discende dal TLC.

I valori stimati per i parametri risultano allora

u1 <- as.numeric(d1)
mu0 <- mean(u1)
sigma0 <- sd(u1)
se0 <- sigma0/sqrt(5)
c(mu0=mu0, sigma0=sigma0, se0=se0)
        mu0      sigma0         se0 
0.102375000 0.008503606 0.003802928

Possiamo allora passare alla Fase II, in cui impostiamo come obiettivo ARL IC = 1000. Come primo approccio, valutiamo la bontà si una carta di controllo di Shewhart per la media. I limiti di controllo risultano

B <- 1000
LCL <- qnorm(1/(2*B), mu0, se0)
UCL <- qnorm(1-1/(2*B), mu0, se0)
c(LCL=LCL, UCL=UCL)
       LCL        UCL 
0.08986136 0.11488864

ARL IC = 1000 significa che ad ogni tempo \(FAP = \frac{1}{B}\), dunque la parte che sta fuori dai limiti di controllo è un millesimo della normale. Infatti

B*(pnorm(LCL, mu0, se0) + pnorm(UCL, mu0, se0, lower.tail=FALSE))
[1] 1

Per quanto riguarda l’EDD, si ha \(EDD = \frac{1}{\theta_1}\) con \(\theta_1\) probabilità di vero allarme al tempo \(t\). Nel nostro caso

salti <- c(0.005, 0.02)
theta1 <- pnorm(LCL, mu0+salti, se0) + pnorm(UCL, mu0+salti, se0, lower.tail=F)
1/theta1
[1] 41.504827  1.025116

Il risultato è soddisfacente per il salto più grande, ma inaccettabile per quello più piccolo. In effetti, questo comportamento rispecchia le caratteristiche delle carte di Shewhart che, non avendo memoria, sono efficaci su salti grandi ma non molto su quelli più piccoli.

Proviamo allora ad implementare una EWMA per la media. Scriviamo una funzione che, presi in input salto standardizzato e ARL IC desiderata, trova il \(\lambda\) che minimizza l’ARL OC.

library(spc)
xewma.opt <- function(mu, B) {
  optimize(function(l) {
    L <- xewma.crit(l, B, sided="two")
    xewma.arl(l, L, mu, sided="two")  # calcola ARL OC
  },
  lower=0, upper=1)$minimum
}
mu <- salti  / (sigma0/sqrt(n))  # salti standardizzati
# ottimizziamo per il salto piccolo
lambda <- xewma.opt(mu[1], B)
L <- xewma.crit(lambda, B, sided="two")
ARL005 <- xewma.arl(lambda, L, mu=mu[1], sided="two")
ARL020 <- xewma.arl(lambda, L, mu=mu[2], sided="two")
c(lambda=lambda, L=L, ARL005=ARL005, ARL020=ARL020)
   lambda      L.cE    ARL005    ARL020 
0.1787671 3.1692153 7.5664301 1.6169934

Si noti che aumentando \(\lambda\) aumentano le prestazioni dell’EWMA nell’identificare velocemente salti grandi (in quanto si avvicina al comportamento di una carta di Shewhart). Provando altri valori si modificano gli EDD per i due salti, in particolare \(\lambda = 0.3\) soddisfa le condizioni poste dall’azienda.

Applichiamo ora questa carta di controllo

# costante di lisciamento
lambda <- 0.3
# valore critico
L <- xewma.crit(lambda, B, sided="two")
## limiti di controllo
LCL <- mu0-L*sigma0*sqrt(lambda/(2-lambda))/sqrt(5)
UCL <- mu0+L*sigma0*sqrt(lambda/(2-lambda))/sqrt(5)
## medie campionarie dei sottogruppi futuri
xbar <- colMeans(matrix(u[R$lotto>32],5))
# calcolo della statistica di controllo
# ci fermiamo la prima volta lo schema segnala un allarme
m <- mu0
w <- NULL
for (i in seq_along(xbar)) {
  m <- lambda*xbar[i]+(1-lambda)*m
  w <- c(w, m)
  if ((m<LCL) || (m>UCL)) break
}
matplot(32+seq_along(w), cbind(xbar[seq_along(w)], w, mu0, LCL, UCL),
        type=c("p", "b", "l", "l", "l"),
        lty=c("solid", "solid", "dotted", "dashed", "dashed"),
        col=c("gray", "maroon", "gray", "gray", "gray"),
        lwd=2, pch=1, xlab="lotto", ylab="")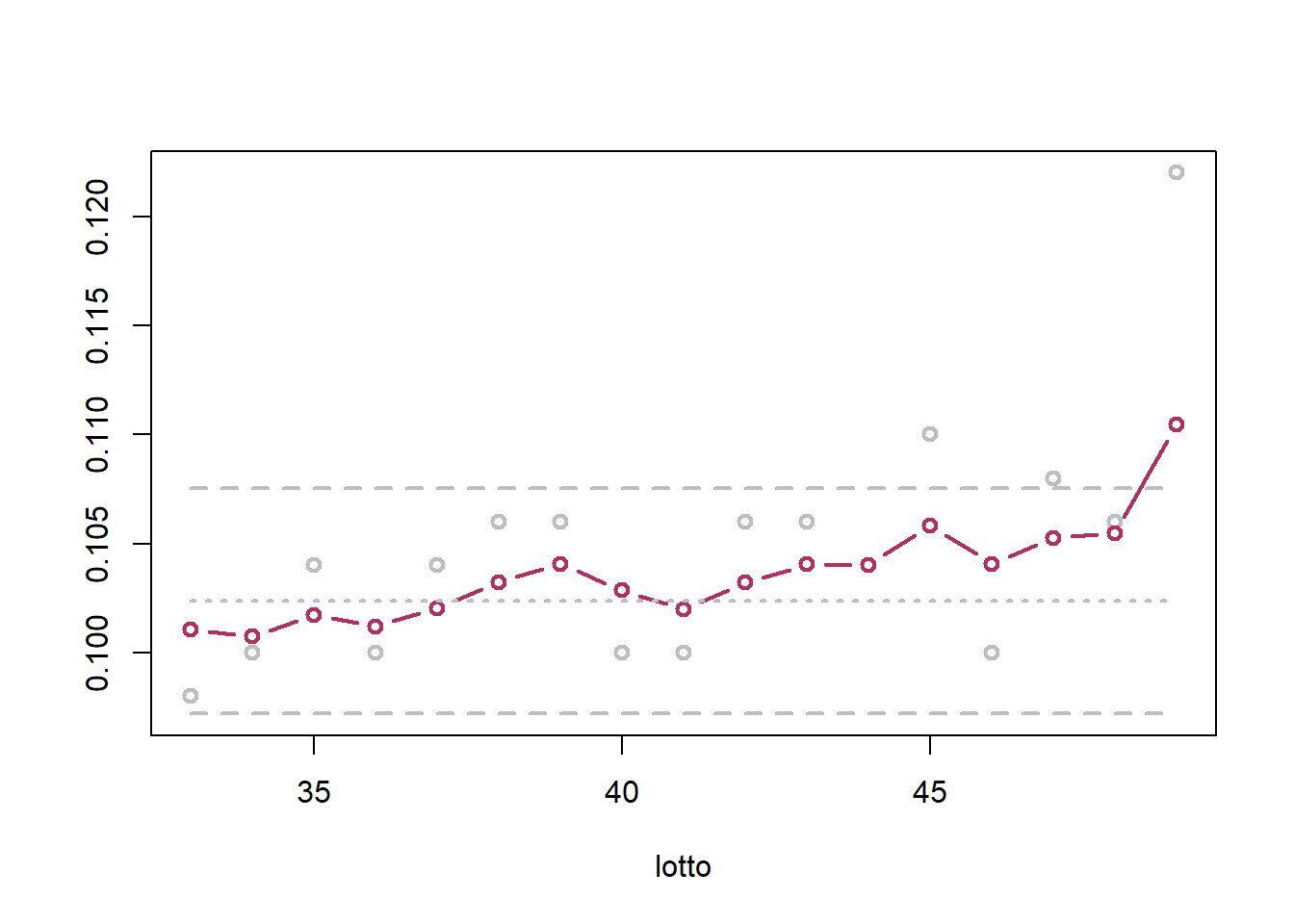

Sulla base di quanto visto nel Caso 4, l’allarme segnalato è corretto ed ha un ritardo di 7/8 lotti.

Caso 11: I cardiochirurghi ci piacciono di più se sono in controllo!

I dati si riferiscono a 146 sessioni operatorie consecutive, effettuate in giorni differenti. x rappresenta il numero di morti, n il numero di pazienti operati in una certa sessione. Per ogni paziente è calcolato prima dell’operazione l’indice di Parsonnet, che è una misura del rischio di morte dovuta all’operazione. Per quanto ci riguarda assumiamo che, da studi precedenti, si abbia \[ \text{Prob}(\text{morte} \mid \text{Parsonnet}) = \frac{1}{1 + e^{3.68 - 0.077 \cdot \text{Parsonnet}}} \]

d <- read.table("~/Uni/Controllo/Datasets/cardio")
str(d)
'data.frame':   146 obs. of  11 variables:
 $ x         : int  0 1 0 0 1 1 0 0 0 0 ...
 $ n         : int  5 3 4 6 1 1 6 6 4 6 ...
 $ Parsonnet1: int  3 62 1 1 56 67 3 8 7 18 ...
 $ Parsonnet2: int  3 1 7 6 NA NA 2 7 7 0 ...
 $ Parsonnet3: int  4 5 1 10 NA NA 3 5 0 5 ...
 $ Parsonnet4: int  4 NA 12 1 NA NA 1 3 2 3 ...
 $ Parsonnet5: int  1 NA NA 5 NA NA 1 3 NA 0 ...
 $ Parsonnet6: int  NA NA NA 7 NA NA 7 5 NA 1 ...
 $ Parsonnet7: int  NA NA NA NA NA NA NA NA NA NA ...
 $ Parsonnet8: int  NA NA NA NA NA NA NA NA NA NA ...
 $ Parsonnet9: int  NA NA NA NA NA NA NA NA NA NA ...

Vogliamo rilevare velocemente aumenti della mortalità nelle sessioni operatorie. La probabilità di morte di ogni paziente è una Bernoulli la cui probabilità di “successo” (termine infelice nel contesto) dipende dall’indice di Parsonnet, come appena visto. Dato che ogni paziente ha diverse probabilità, la distribuzione del conteggio dei morti in una sessione non è una Binomiale.

Distribuzione marginale dei morti

theta <- 1/(1+exp(3.68-0.077*d[,3:11]))
c(Attesi=sum(theta, na.rm=TRUE), SD=sqrt(sum(theta*(1-theta), na.rm=TRUE)))
   Attesi        SD 
52.502589  5.703836

Utilizziamo una carta EWMA unilaterale così definita: \[ W_t = \begin{cases} 0 & \text{if } t = 0 \\ \max \left[ 0, \lambda \left( \frac{x_t - m_t}{n_t} \right) + (1 - \lambda) W_{t-1} \right] & \text{if } t = 1, 2, \ldots \end{cases} \]

dove \(m_t\) indica la media in controllo di \(x_t\). Anche un CuSum sarebbe stato una scelta possibile, anche se meno interpretabile. In pratica aggiungiamo la excess mortality del giorno \(t\) ripesata per il numero di pazienti operati.

Ci accostiamo sul compromesso di \(\lambda = 0.2\) e ARL = 100. Il limite di controllo sarà il quantile \(1 - 1/B\) di della distribuzione di \(W_t\) condizionata al fatto che non sono stati segnalati allarmi dei tempi precedenti. Questi vanno calcolati via simulazione e dinamicamente per ogni gruppo di pazienti dai loro indici di Parsonnet.

In pratica, si generano \(N_{sim}\) simulazioni parallele della statistica EWMA (\(W^*_t\)) allo scorrere del tempo. Ad ogni sessione t, queste si aggiornano usando i dati di rischio dei pazienti correnti, assumendo sempre che il processo sottostante sia in controllo. Il limite \(L_t\) è il quantile \((1-1/B)\) dei valori correnti di \(W^*_t\). Inoltre le traiettorie simulate \(W^*_t\) che superano \(L_t\) vengono successivamente sostituite campionando da quelle che sono rimaste sotto \(L_t\), per assicurare che la stima del quantile per le sessioni future si basi sempre su percorsi che, fino a quel momento, non avrebbero segnalato un allarme.

Una implementazione è come segue

# dati n valori di probabilità di morte, restituisce Nsim generazioni
# del conteggio giornaliero dei morti (x_t1*, x_tNsim*)
rx <- function(Nsim, theta) {
  n <- length(theta)
  # per ogni paziente simulo Nsim volte se muore 
  # (muore se il suo runif(0,1) < theta)
  # sommo per ottenere il conteggio giornaliero
  colSums(matrix(runif(Nsim*n), n) < theta)
}

## Inizializzazione
lambda <- 0.2
B <- 100
Wt <- 0
Nsim <- 100*B
Wstar <- rep(0,Nsim)
## Vettori per memorizzare la statistica
## e i limiti di controllo
W <- L <- numeric(NROW(d))
## Ciclo sulle sessioni operatorie
for (t in 1:NROW(d)) {
  ## DATI REALI (per le barrette nere)
  # dati raccolti al tempo t
  xt <- d[t,1]
  nt <- d[t,2]
  # probabilità morte in controllo operazioni al tempo t
  thetat <- 1/(1+exp(3.68-0.077*unlist(d[t, 2+(1:nt)])))
  # media in controllo di xt
  mt <- sum(thetat)
  # Wt
  Wt <- max(0, lambda*(xt-mt)/nt+(1-lambda)*Wt)
  
  ## DATI SIMULATI (per il calcolo dei limiti)
  # Wstar: Nsim traiettorie dai dati simulati
  Wstar <- pmax(0, lambda*(rx(Nsim, thetat)-mt)/nt+(1-lambda)*Wstar)
  # Limiti
  Lt <- quantile(Wstar, 1-1/B)
  # Sostituzione Wstar > Lt con Wstar <= Lt
  idx <- which(Wstar>Lt)
  Wstar[idx] <- sample(Wstar[Wstar<=Lt], length(idx))
  # Memorizzazione dei risultati
  W[t] <- Wt
  L[t] <- Lt
}
matplot(cbind(W,L), type=c("h","s"),
        xlab="sessione operatoria",
        ylab="eccesso mortalità per intervento")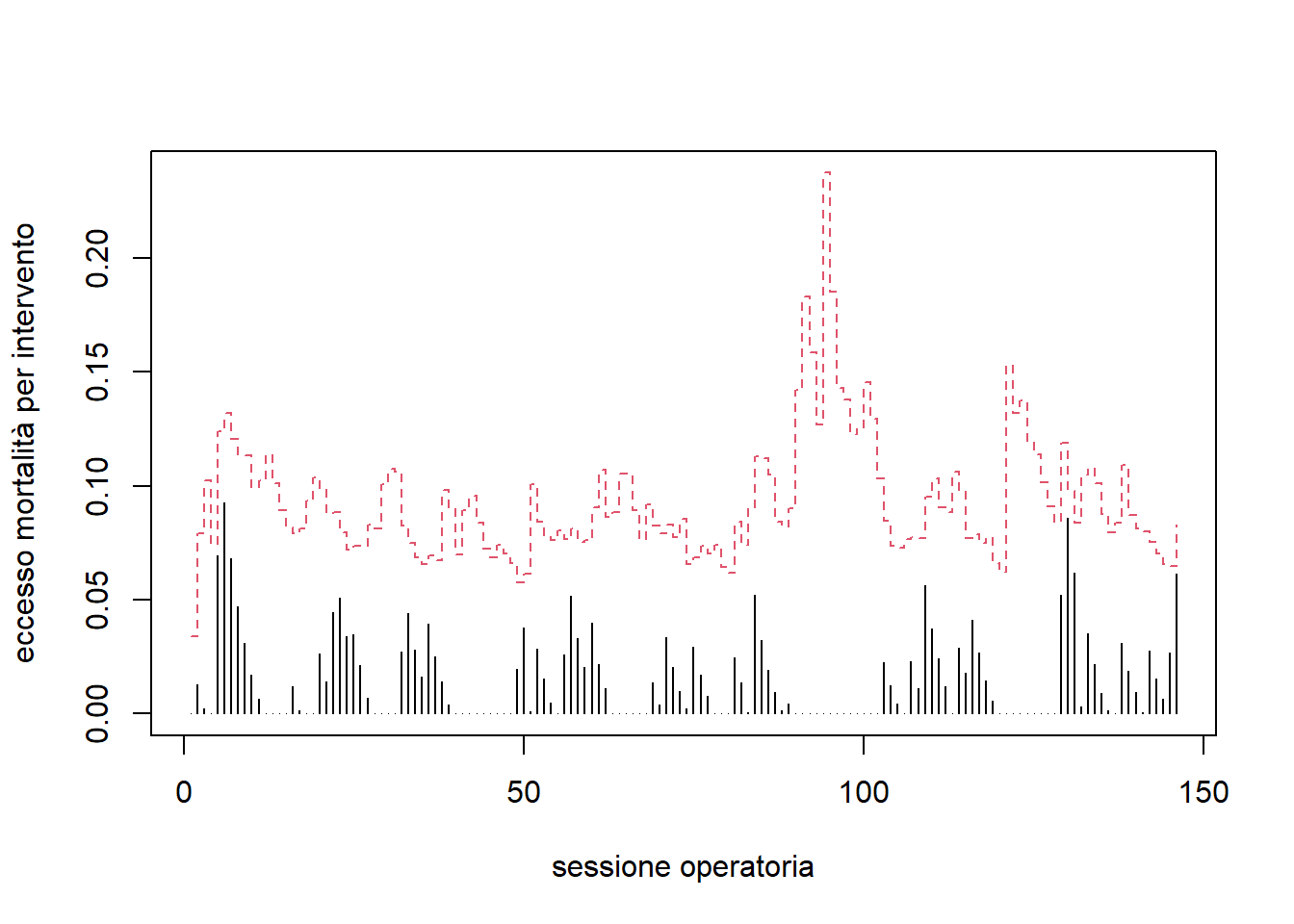

Si noti che i limiti risultati sono dunque aleatori, anche se per \(N_{sim}\) grande la loro stima è piuttosto precisa.

Caso 12: Sul controllo del numero di non conformità in una industria tessile

I dati si riferiscono ad una linea di produzione di una industria tessile che produce tessuti di cotone con tessitura, peso e colore differente. Il tessuto viene fotografato man mano che è prodotto, e un sistema automatico riconosce la presenza di eventuali non regolarità del tessuto stesso. nc numero di non conformità rilevate, mq metri quadri prodotti.

d <- read.table("~/Uni/Controllo/Datasets/tessuto")
str(d)
'data.frame':   159 obs. of  2 variables:
 $ nc: int  4 1 1 1 0 1 0 1 0 0 ...
 $ mq: int  1150 590 270 270 200 200 200 200 200 200 ...

È ragionevole assumere \[ nc \sim Po(u_0 mq) \]

con \(u_0 = 0.0023\) noto e indipendenza tra i cicli di produzione.

Vogliamo implementare un CuSum con ARL = 400 e che rilevi velocemente un raddoppio del tasso di non conformità. La statistica di controllo risulta \[ W_t = \begin{cases} 0 & \text{if } t = 0 \\ \max \left( 0, W_{t-1} + \log \left( \frac{p(nc_t; 2 \cdot u_0 \cdot m_{q_t})}{p(nc_t; u_0 \cdot m_{q_t})} \right) \right) & \text{if } t = 1, 2, \ldots \end{cases} \]

Il procedimento è analogo a quello del caso precedente, con l’utilizzo di limiti dinamici.

Caso 13: Sulla capacità di forare il metallo con il giusto angolo ed un’altra storia che riguarda \(C_p\)

Una azienda produce piccole parti di metallo che devono essere forate ad un angolo preciso con la superficie orizzontale della parte. L’azienda valuta l’acquisto di una nuova macchina che produce i fori con un procedimento di elettrotensione. Sono state eseguite 50 misurazioni di prova, sulle quali vogliamo calcolare la capacità potenziale dell’apparecchio.

x <-scan("~/Uni/Controllo/Datasets/edm")
str(x)
 num [1:50] 46 45.2 45.3 44.7 44.1 ...

Un angolo è considerato buono se è nell’intervallo \(44^\circ \pm 2^\circ\).

L’ipotesi di normalità è accettabile e il test t \(H_0: \mu = 44\) non rifiuta l’ipotesi nulla. Dunque, possiamo assumere che il processo sia centrato e calcolarne il \(C_p\):

s <- sd(x)
LSL <- 44 - 2
USL <- 44 + 2
Cp.hat <- (USL - LSL) / (6 * s)
Cp.hat
[1] 0.6778377

Il valore è decisamente basso, in quanto circa un terzo della variabilità naturale del processo finisce fuori dai limiti di specifica. Dall’intervallo di confidenza per lo scarto quadratico medio possiamo ottenere facilmente l’intervallo per \(C_p\), che risulta

n <- length(x)
alpha <- 0.01
c(
A = Cp.hat * sqrt(qchisq(alpha / 2, n - 1) / (n - 1)),
B = Cp.hat * sqrt(qchisq(1 - alpha / 2, n - 1) / (n - 1))
)
        A         B 
0.5054820 0.8564781

Anche nella migliore delle ipotesi, la capacità del processo non è soddisfacente (se proprio non siamo stati sfigati). Dunque, l’azienda decide di non acquistare il nuovo macchinario perché ritenuto insoddisfacente (si vorrebbe \(C_p \ge 1.5\)).

Si noti che alla stessa conclusione si sarebbe potuti arrivare valutando la proporzione di non conformi ottenuta dalla stima dello scarto quadratico medio, sotto ipotesi di normalità.

Gli indici di capacità sono utili nel dimostrare, non lo avreste mai detto, le capacità di un processo. Ad esempio, una azienda produce \(n\) parti di una caratteristica con LSL=32, USL=36, per dimostrarne la qualità ad un possibile acquirente. Si vuole verificare \(H_0: C_p \ge 2\) sotto i vicoli che la probabilità di errore del secondo tipo per \(C_p=1.5\) e di errore di primo tipo per \(C_p=2\) siano entrambe minori o uguali all’1%. Si noti che un errore di primo tipo danneggerebbe il fornitore, mentre di secondo tipo l’acquirente. Chiaramente, un’ipotesi su \(C_p\) con LSL e USL fissati corrisponde ad una certa ipotesi su \(\sigma\). Sotto normalità possiamo ricorrere alla usuale distribuzione \[ T = \frac{(n-1)s^2}{\sigma_0^2} \sim \chi^2_{n-1} \]

Definiamo allora la funzione potenza \(U(\gamma)\), che rappresenta la probabilità di rifiutare \(H_0: C_p \ge \gamma_0\) al variare di \(\gamma\). Non ho voglia di scrivere il LaTeX del resto…

Si ha

alpha <- 0.01
beta <- 0.01
gamma0 <- 2
gamma1 <- 1.5
omega2 <- (gamma0 / gamma1)^2
nmax <- 10000
n <- 2:nmax
L <- qchisq(1 - alpha, n - 1)
U <- 1 - pchisq(L / omega2, n - 1)
i <- min(which(U > 1 - beta))
c(n = n[i], L = L[i], U = U[i])
          n           L           U 
133.0000000 172.7108244   0.9900274

Per rispettare il vincolo sull’errore di secondo tipo il campione dovrebbe essere di 133 unità. E l’altro vincolo? Boh.

Caso 14: Sulla capacità dei laminati plastici di resistere alle flessioni (per non parlare della sua sorveglianza)

I dati sono quelli del Caso 1, almeno non devo imparare un’altra storia.

x <- scan("~/Uni/Controllo/Datasets/plastic-strength")
str(x)
 num [1:125] 140 139 144 141 136 ...
LSL <- 130 # Pascal
USL <- 155 # Pascal

L’ipotesi di normalità è accettabile, tuttavia il test t mostra che il processo è chiaramente non centrato: utilizzeremo \(C_{pk}\)

mu0.hat <- mean(x)
sigma0.hat <- sd(x)
Cpl.hat <- (mu0.hat - LSL) / (3 * sigma0.hat)
Cpu.hat <- (USL - mu0.hat) / (3 * sigma0.hat)
Cpk.hat <- min(Cpl.hat, Cpu.hat)
c(
mu0.hat = mu0.hat, sigma0.hat = sigma0.hat,
Cpl = Cpl.hat, Cpu = Cpu.hat, Cpk = Cpk.hat
)
   mu0.hat sigma0.hat        Cpl        Cpu        Cpk 
139.870400   2.020940   1.628021   2.495473   1.628021

Il processo sembra capace 👏. Si consideri che per le proprietà di \(C_{pk}\) la capacità del processo è ancora maggiore, nel senso che la coda di destra è praticamente del tutto nell’intervallo di specifica.

Lo standard error di \(\hat{C}_{pk}\) si ottiene da

Cpk.se <- sqrt(1 / (9 * length(x)) 
               + Cpk.hat * Cpk.hat / (2 * length(x) - 2))
c(Cpk.hat = Cpk.hat, Cpk.se = Cpk.se)
  Cpk.hat    Cpk.se 
1.6280215 0.1075928

Non mi si chieda perché vengono numeri diversi che al Masarots. Il processo è certamente capace.

La taratura dell’impianto su una particolare media ha un certo margine di errore, dunque non possiamo assumere di conoscere la media IC, solo che questa sia costante a periodi. Siccome la capacità è comunque buona anche per medie leggermente starate, vogliamo usare come riferimento la capacità del processo e non la sua media. Per la sorveglianza, l’azienda utilizza quindi un CuSum a tre zone, in cui si vuole una segnalazione veloce per \(C_{pk} \le 1.3\), nessuna segnalazione per \(C_{pk} \ge 1.7\) e si è indifferenti per \(1.3 < C_{pk} < 1.7\). Queste ipotesi si traducono banalmente in tre equivalenti per la media. In particolare, il processo è capace se la media è nell’intervallo

mu0L <- LSL+3*1.7*sigma0.hat
mu0U <- USL-3*1.7*sigma0.hat
c(mu0L, mu0U)
[1] 140.3068 144.6932

Mentre non lo è se sta fuori dall’intervallo

mu1L <- LSL+3*1.3*sigma0.hat
mu1U <- USL-3*1.3*sigma0.hat
c(mu1L, mu1U)
[1] 137.8817 147.1183

Caso 15: Sul diametro dei tubicini di gomma di una apparecchiatura elettromedicale

Tu volevi solo tubicini, tubicini, tubicini…

I dati rappresentano le misure del diametro, in mm, di 411 tubicini di gomma prodotti mentre il processo era considerato in controllo. Per essere fissato correttamente all’apparecchiatura medica per cui è progettato, il diametro deve stare nell’intervallo \(2mm \pm 0.1mm\)

x <- scan("~/Uni/Controllo/Datasets/tubicini")
str(x)
 num [1:411] 1.98 1.96 1.98 1.96 1.98 ...

Calcoliamo \(C_{pk}\)

LSL <- 2 - 0.1
USL <- 2 + 0.1
mu.hat <- mean(x)
sigma.hat <- sd(x)
Cpl.hat <- (mu.hat - LSL) / (3 * sigma.hat)
Cpu.hat <- (USL - mu.hat) / (3 * sigma.hat)
Cpk.hat <- min(Cpl.hat, Cpu.hat)
Cpk.se <- sqrt(1 / (9 * length(x)) + Cpk.hat * Cpk.hat / (2 * length(x) - 2))

c(
  Cpk.hat = Cpk.hat, Cpl.hat = Cpl.hat, Cpu.hat = Cpu.hat
)
 Cpk.hat  Cpl.hat  Cpu.hat 
1.657630 1.657630 2.137728 
z <- qnorm(1 - 0.05 / 2)
c(
  Cpk.conf.int.low = Cpk.hat - z * Cpk.se,
  Cpk.conf.int.up = Cpk.hat + z * Cpk.se
)
Cpk.conf.int.low  Cpk.conf.int.up 
        1.539685         1.775574

La capacità del processo appare buona. Tuttavia, la distribuzione è decisamente asimmetrica, al punto di rifiutare con forza l’ipotesi di normalità. Pertanto, le assunzioni alla base della procedura appena vista non sono rispettate.

hist(x, prob = TRUE)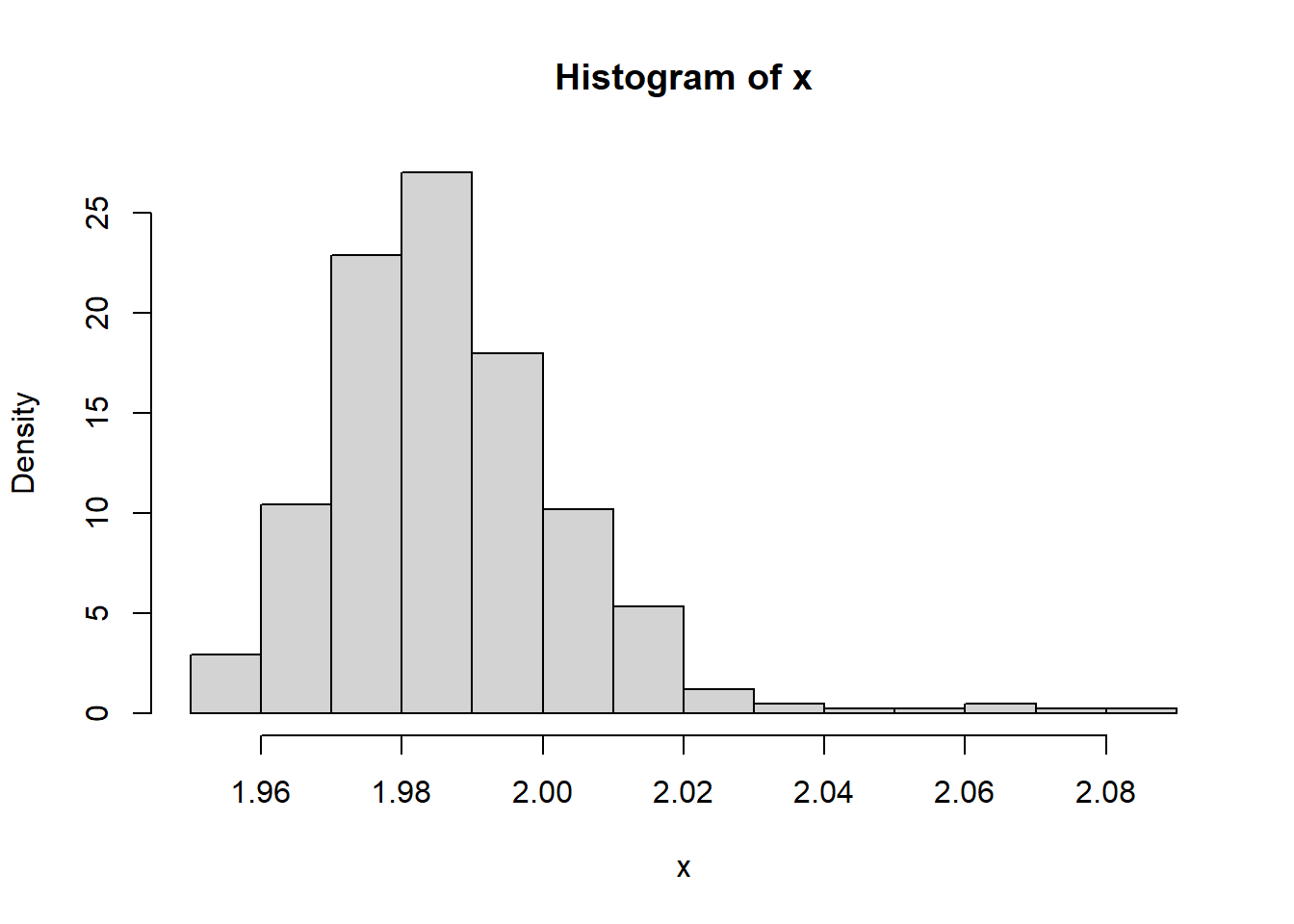

\(C_{pk}\) è facilmente estendibile a qualsiasi distribuzione, sostituendo la mediana della distribuzione alla media e \(Q_{0.00135}\) a \(3\sigma_0\). Tuttavia, quest’ultimo quantile è piuttosto estremo, il ché ne rende particolarmente difficile la stima per \(n\) non grande: è opportuno rifarsi comunque ad un’assunzione parametrica. Diverse opzioni sono possibili, noi seguiamo la strada della \(\lambda\) generalizzata di Tukey. Questa distribuzione risulta molto flessibile perché governata da 4 parametri, due che ne determinano posizione e variabilità e due la forma. Le funzioni di densità e ripartizione non hanno una espressione esplicita.

In R l’implementazione è ottenuta dalle solite funzioni [d,p,q,r]gl, della libreria gld. Possiamo divertirci a osservare come cambia la distribuzione al variare dei diversi parametri, lo omettiamo per brevità.

Per l’implementazione di nostro interesse, la funzione fit.fkml() calcola la SMV dei 4 parametri per i nostri dati

library(gld)
l.hat <- fit.fkml(x)
summary(l.hat)
Generalised Lambda Distribution fkml type. Maximum Likelihood  estimate.

Optim (final) estimates:
Maximum Likelihood estimate, gld type: fkml 
 lambda1   lambda2   lambda3   lambda4  
  1.9840  104.5470    0.2617   -0.1252  
internal g-o-f measure at optim minimum: -2.741591 
optim.details:
Counts: function gradient 
     395       NA 
Convergence: [1] 0
Message: NULL

Vediamo come la distribuzione parametrica si sovrappone alla nostra distribuzione empirica. Possiamo farlo, ovviamente, tramite funzione di densità o di ripartizione

## per prima cosa estraiamo le stime dei lambda
ll <- l.hat$lambda
ll
    lambda1     lambda2     lambda3     lambda4 
  1.9840226 104.5470444   0.2617400  -0.1252063 
## poi costruiamo il grafico
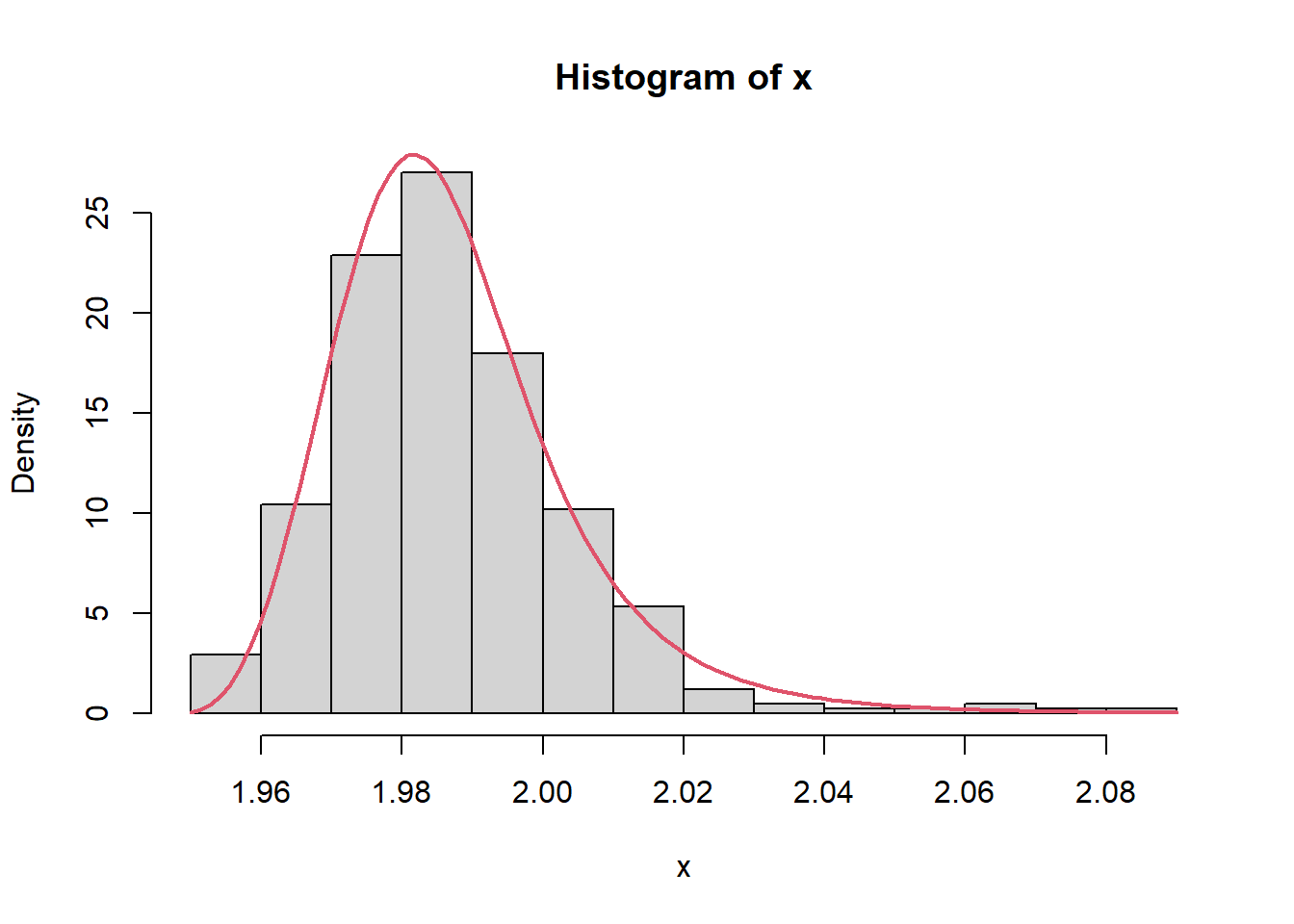
hist(x, prob = TRUE)
curve(dgl(x, ll[1], ll[2], ll[3], ll[4]),
      lwd = 2, col = 2, add = TRUE
)

plot(ecdf(x))
curve(pgl(x, ll[1], ll[2], ll[3], ll[4]), min(x), max(x),
      lwd = 2, col = "red", add = TRUE
)

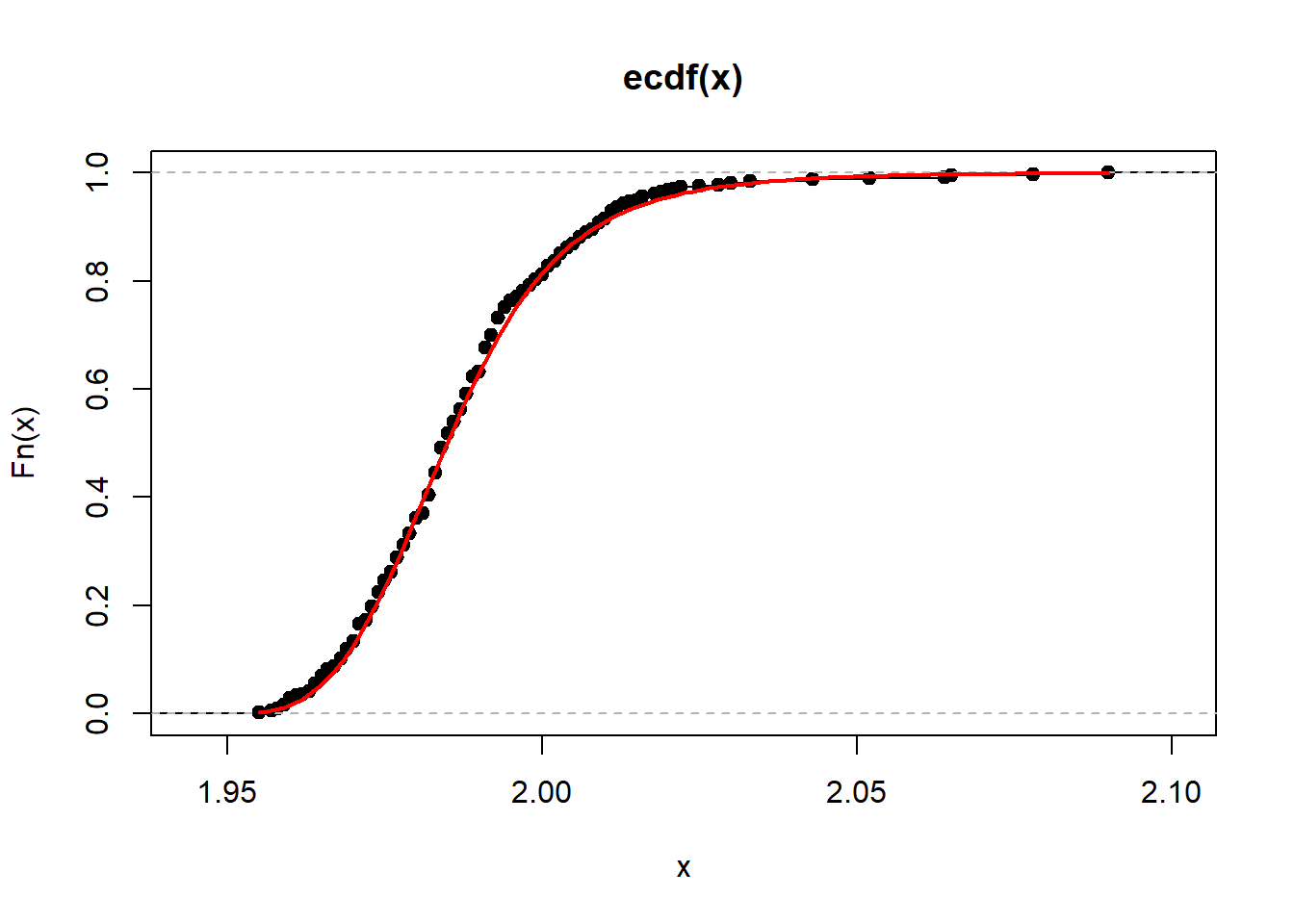
L’adattamento è del tutto soddisfacente. Possiamo ora calcolare \(C_{pk}\) assumendo questa distribuzione.

ll <- l.hat$lambda
p <- c(0.00135, 0.5, 1 - 0.00135)
q <- qgl(p, ll[1], ll[2], ll[3], ll[4])
Cpl.hat <- (q[2] - LSL) / (q[2] - q[1])
Cpu.hat <- (USL - q[2]) / (q[3] - q[2])
Cpk.hat <- min(Cpl.hat, Cpu.hat)
c(Cpk.hat = Cpk.hat, Cpl.hat = Cpl.hat, Cpu.hat = Cpu.hat)
 Cpk.hat  Cpl.hat  Cpu.hat 
1.181175 2.746030 1.181175

L’indice così ottenuto è decisamente inferiore rispetto a quello sotto ipotesi di normalità, al punto da trasformare un processo che appariva dalle ottime performance in uno appena sopra la soglia della decenza.

hist(x, nclass = 20, prob = TRUE, xlim = c(1.9, 2.1), ylim = c(0, 30))
curve(dgl(x, ll[1], ll[2], ll[3], ll[4]), 1.9, 2.1,
      col = 2, lwd = 2, add = TRUE)
curve(dnorm(x, mu.hat, sigma.hat), 1.9, 2.1,
      col = 3, lwd = 2, add = TRUE)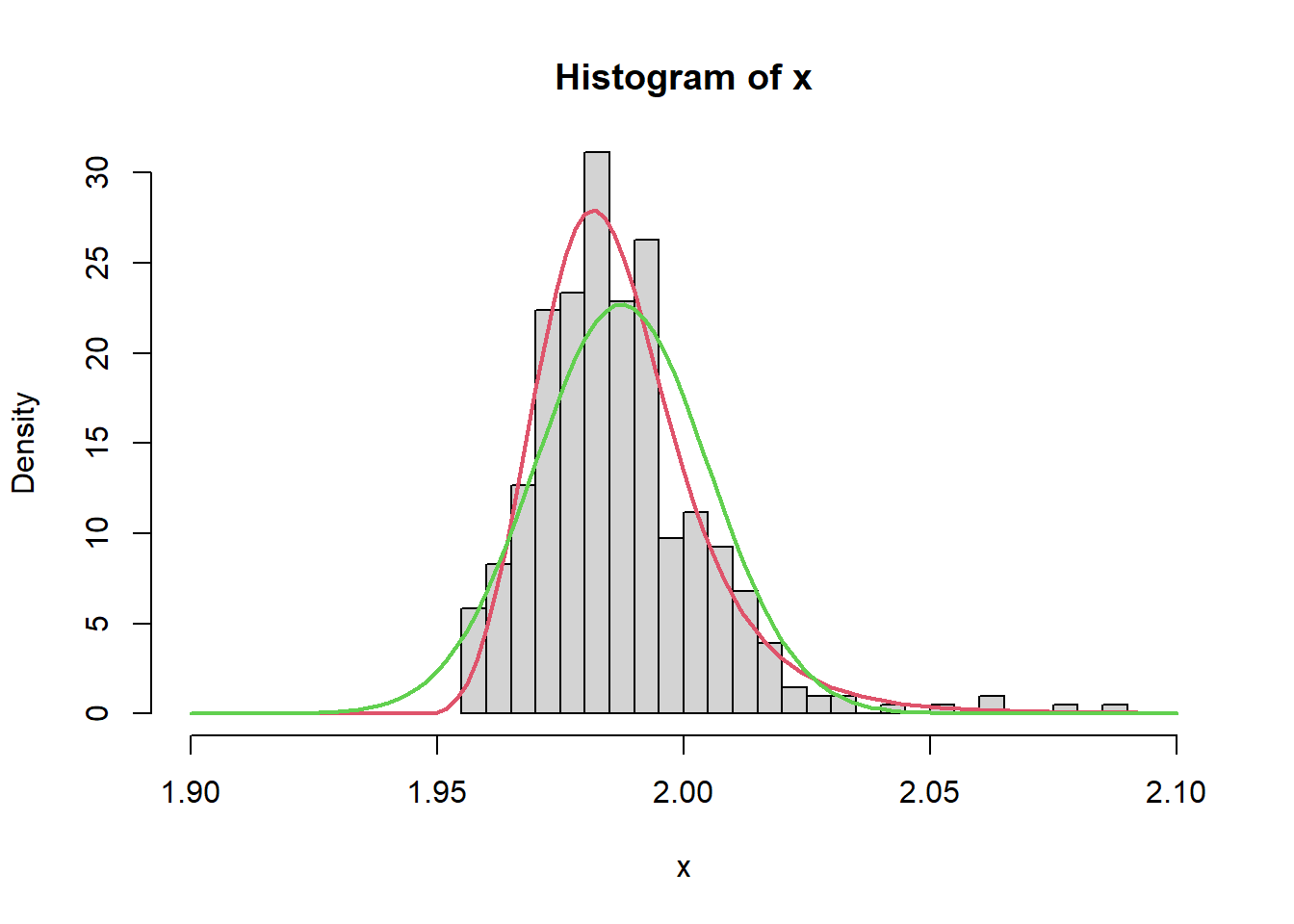

Si noti come sotto normalità fosse la coda sinistra a risultare più problematica, vista la simmetria della distribuzione e il fatto che la media stimata sta a sinistra del centro dell’intervallo di specifica. Sotto questa nuova distribuzione, invece, è la coda destra ad avvicinarsi pericolosamente al limite, in quanto questa è piuttosto pesante.

Per un intervallo di confidenza per \(C_{pk}\) seguiamo una procedura bootstrap. Generiamo 200 campioni di 411 unità dalla distribuzione stimata e, per ognuno, calcoliamo l’indice \(C_{pk}\). Dopodiché prendiamo come intervallo di confidenza i valori nel 95% centrale della distribuzione.

n <- length(x)
l.star <- replicate(30, fit.fkml(rgl(n, ll[1], ll[2], ll[3], ll[4]))$lambda)
q.star <- apply(l.star, 2,
                function(ll) qgl(p, ll[1], ll[2], ll[3], ll[4])
)
Cpl.star <- apply(q.star, 2, function(q) (q[2] - LSL) / (q[2] - q[1]))
Cpu.star <- apply(q.star, 2, function(q) (USL - q[2]) / (q[3] - q[2]))
Cpk.star <- pmin(Cpl.star, Cpu.star)
boxplot(Cpk.star, Cpl.star, Cpu.star)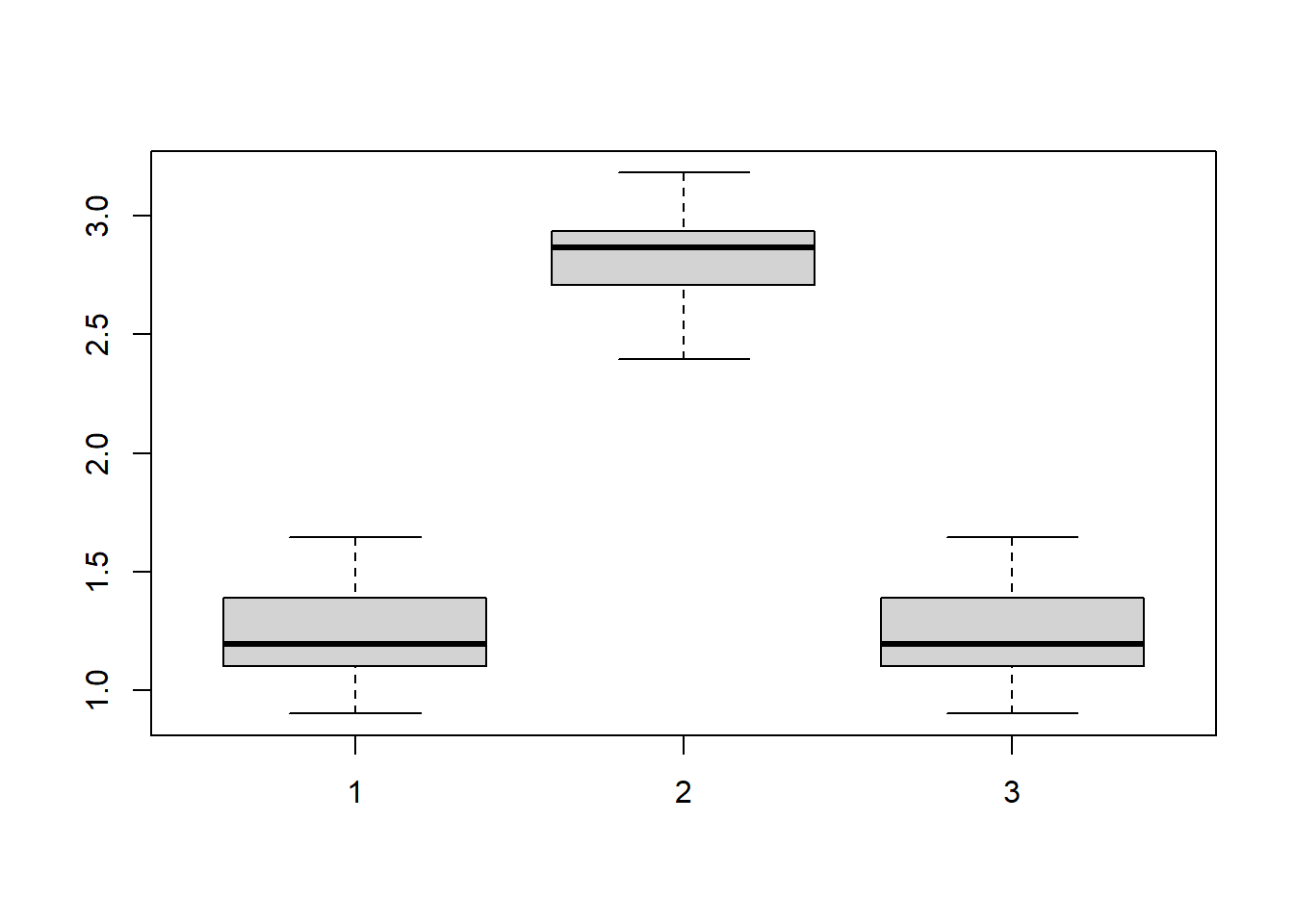

quantile(Cpk.star, c(0.025, 0.975))
     2.5%     97.5% 
0.9103264 1.5822938

È possibile che l’indice sia in realtà addirittura minore di 1. Si noti che l’asimmetria è tale che una piccola diminuzione della media porterebbe ad un aumento della capacità del processo.

Caso 16: Sulla capacità di misurare la durezza dei metalli

Per valutare le prestazioni di un nuovo durometro (che misura la durezza dei metalli) si sono effettuate due misurazioni per parte su 20 diverse parti di acciaio scelte casualmente.

dati <- read.table("~/Uni/Controllo/Datasets/durezza")
str(dati)
'data.frame':   40 obs. of  2 variables:
 $ durezza: num  2.1 2 2.4 2.3 2 2.1 2.7 2.7 1.9 1.8 ...
 $ parte  : int  1 1 2 2 3 3 4 4 5 5 ...

Si vuole valutare la capacità dello strumento di eseguire misure replicabili, in particolare in confronto all’ampiezza dell’intervallo di specifica.

LSL <- 0.5
USL <- 6.0
plot(dati$durezza[seq(1, 40, by = 2)], dati$durezza[seq(2, 40, by = 2)])
abline(a = 0, b = 1, lty = "dotted", lwd = 2)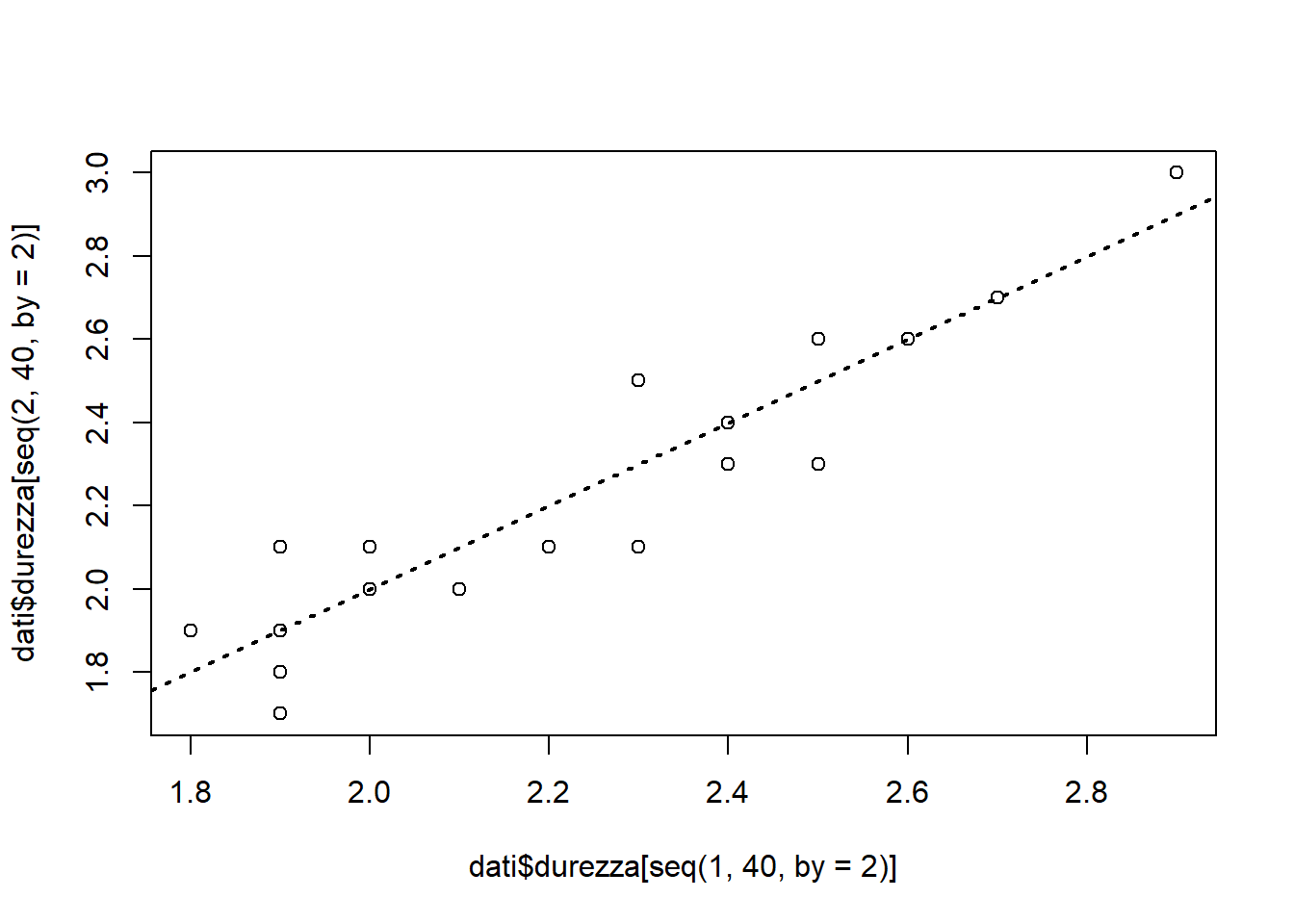

In questo grafico ci aspetteremmo dati sulla bisettrice per misure perfette. Emerge che la fonte principale di variabilità è quella tra parte e parte, non quella di misura.

Risvegliando qualche trauma da Modelli 2, proviamo a fittare un modello ad effetti casuali

library(lme4)
m <- lmer(durezza ~ (1 | parte), dati)
summary(m)
Linear mixed model fit by REML ['lmerMod']
Formula: durezza ~ (1 | parte)
   Data: dati

REML criterion at convergence: -14.2

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-1.34218 -0.62313  0.07412  0.50977  1.22882 

Random effects:
 Groups   Name        Variance Std.Dev.
 parte    (Intercept) 0.09557  0.3091  
 Residual             0.00750  0.0866  
Number of obs: 40, groups:  parte, 20

Fixed effects:
            Estimate Std. Error t value
(Intercept)  2.23000    0.07047   31.64
ci <- confint(m)
ci
                 2.5 %    97.5 %
.sig01      0.22346647 0.4296080
.sigma      0.06539166 0.1223429
(Intercept) 2.08865096 2.3713490
v <- as.data.frame(VarCorr(m))
v
       grp        var1 var2       vcov      sdcor
1    parte (Intercept) <NA> 0.09556579 0.30913717
2 Residual        <NA> <NA> 0.00750000 0.08660254
v[2, 4] / (v[1, 4] + v[2, 4])
[1] 0.07276905

Notiamo le differenze tra la varianza tra le parti e tra le misure (residual) e i corrispettivi intervalli di confidenza. La varianza dovuta all’errore di misura sul totale della varianza tra le misure rappresenta circa il 7%, mentre il rimanente è spiegato dalla differenza tra le parti. Questo risultato è sufficientemente soddisfacente. Non vi sono indicazioni contro la normalità dei residui.

Un indice usato per comunicare la dimensione degli errori di misura rispetto all’ampiezza dell’intervallo di specifica è \[ \frac{P}{T} = \frac{\text{precisione}}{\text{tolleranza}} = \frac{6\sigma_{ripetibilità}}{USL-LSL} \]

Consideriamo buoni valori \(\frac{P}{T} \le 0.01\) e inaccettabili \(\frac{P}{T} > 0.3\). Nel nostro caso

6 * c(est = v[2, 5], ci[2, ]) / (USL - LSL)
       est      2.5 %     97.5 % 
0.09447550 0.07133635 0.13346494

È accettabile se la capacità del processo è grande. In effetti, se siamo ragionevolmente distanti dai limiti di specifica anche questo livello di errore è tollerabile nel senso che la probabilità di rifiutare un pezzo buono è estremamente piccola.

Caso 17: Sull’impedenza di alcuni motorini di avviamento

I dati sono misurazioni dell’impedenza termica (in centigradi per Watt * 100) su una unità di potenza di un motorino di avviamento. Sono state misurate 10 parti, ognuna da 3 operatori diversi, con 3 misure per operatore.

dati <- read.table("~/Uni/Controllo/Datasets/impedenza")
str(dati)
'data.frame':   90 obs. of  3 variables:
 $ impedenza: int  37 42 30 42 28 42 25 40 25 35 ...
 $ parte    : int  1 2 3 4 5 6 7 8 9 10 ...
 $ operatore: int  1 1 1 1 1 1 1 1 1 1 ...

Vogliamo valutare riproducibilità e ripetibilità del sistema di misura.

LSL <- 18
USL <- 58
interaction.plot(dati$parte, dati$operatore, dati$impedenza, mean)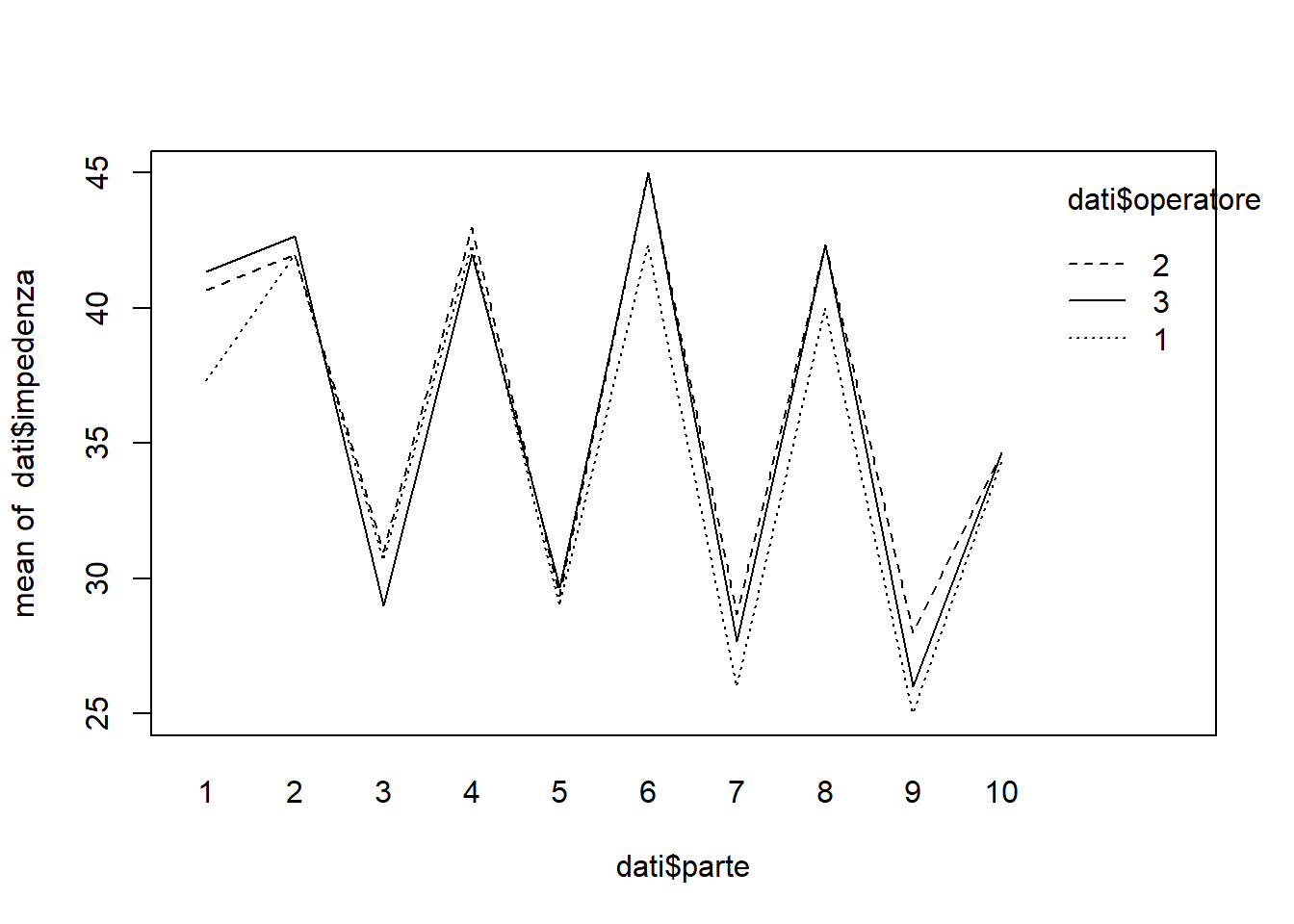

La parte predominante della variabilità sembra essere da parte a parte. L’effetto dell’operazione e l’interazione tra parte e operatore sembrano deboli, but what do i know. Vediamo il modello ad effetti casuali

m <- lmer(impedenza ~
            (1 | parte) +
            (1 | operatore) +
            (1 | parte:operatore), dati)
summary(m)
Linear mixed model fit by REML ['lmerMod']
Formula: impedenza ~ (1 | parte) + (1 | operatore) + (1 | parte:operatore)
   Data: dati

REML criterion at convergence: 295.3

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-1.7855 -0.6265 -0.1573  0.5301  2.0230 

Random effects:
 Groups          Name        Variance Std.Dev.
 parte:operatore (Intercept)  0.7280  0.8532  
 parte           (Intercept) 48.2885  6.9490  
 operatore       (Intercept)  0.5651  0.7517  
 Residual                     0.5111  0.7149  
Number of obs: 90, groups:  parte:operatore, 30; parte, 10; operatore, 3

Fixed effects:
            Estimate Std. Error t value
(Intercept)   35.800      2.247   15.94
v <- as.data.frame(VarCorr(m))
a <- c(
  parte = v[2, 4], "riproducibilità" = v[1, 4] + v[3, 4],
  ripetibilità = v[4, 4], misura = v[1, 4] + v[3, 4] + v[4, 4]
)
cbind(
  var = a, "%" = a / sum(a[1:3]), sd = sqrt(a),
  "6sd/T" = 6 * sqrt(a) / (USL - LSL)
)
                       var          %        sd     6sd/T
parte           48.2884684 0.96398395 6.9489905 1.0423486
riproducibilità  1.2930301 0.02581279 1.1371148 0.1705672
ripetibilità     0.5111079 0.01020326 0.7149181 0.1072377
misura           1.8041381 0.03601605 1.3431821 0.2014773
ci <- confint(m)
ci
                 2.5 %     97.5 %
.sig01       0.5660235  1.3045349
.sig02       4.4860237 11.0523616
.sig03       0.2110260  2.9749455
.sigma       0.6038444  0.8647398
(Intercept) 31.1982104 40.4017893
6 * c(est = v[4, 5], ci[4, ]) / (USL - LSL)  # ripetibilità
       est      2.5 %     97.5 % 
0.10723772 0.09057666 0.12971098 
6 * sqrt(a[4]) / (USL - LSL)  # misura
   misura 
0.2014773

Le prestazioni non sono un granché.

Caso 18: Sul perchè esplorare la superficie di risposta di una reazione chimica è utile

In una industria, una delle fasi produttive è basata su una reazione chimica. Il processo sembra essere stabile ma la resa attuale della reazione (\(y\) nel seguito) è intorno al 40% e ci si chiede se sia il massimo raggiungibile. Sono presenti due covariate, \(X_1\) tempo della reazione e \(X_2\) temperatura. Si vuole capire come modificarle in modo da massimizzare la resa. Per motivi di sicurezza, ad ogni passo non possiamo modificare più di 5 unità ciascuna variabile.

##  X1   X2
X <- matrix(
  c(
    # nuove configurazioni
    30, 150,
    30, 160,
    40, 150,
    40, 160,
    # sulla configurazione attuale
    35, 155,
    35, 155,
    35, 155,
    35, 155,
    35, 155
  ), 9, byrow = TRUE
)

##   y      X1  X2
y <- c(
  39.3, # 30, 150
  40.0, # 30, 160
  40.9, # 40, 150
  41.5, # 40, 160
  40.3, # 35, 155
  40.5, # 35, 155
  40.7, # 35, 155
  40.2, # 35, 155
  40.6  # 35, 155
)

Un primo modello lineare

m1 <- lm(y ~ I(X[, 1] - 35) + I(X[, 2] - 155))
summary(m1)

Call:
lm(formula = y ~ I(X[, 1] - 35) + I(X[, 2] - 155))

Residuals:
      Min        1Q    Median        3Q       Max 
-0.244444 -0.044444  0.005556  0.055556  0.255556 

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)     40.44444    0.05729 705.987 5.45e-16 ***
I(X[, 1] - 35)   0.15500    0.01719   9.019 0.000104 ***
I(X[, 2] - 155)  0.06500    0.01719   3.782 0.009158 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1719 on 6 degrees of freedom
Multiple R-squared:  0.941, Adjusted R-squared:  0.9213 
F-statistic: 47.82 on 2 and 6 DF,  p-value: 0.0002057

Tutti i termini quadratici e di interazione risultano non significativi se aggiunti al modello. Se calcoliamo il gradiente della superficie definita dal modello nel punto corrispondente all’attuale configurazione vediamo in che direzione aumenta la resa

## linee di livello
b <- coef(m1)
x1 <- seq(15, 55, length = 200)
x2 <- seq(135, 175, length = 200)
yhat <- outer(x1, x2,
              function(x1, x2) b[1] + b[2] * (x1 - 35) + b[3] * (x2 - 155)
)
contour(x1, x2, yhat, xlab = expression(x[1]), ylab = expression(x[2]))
## punto corrente
points(35, 155, pch = 20, col = "red")
## gradiente
arrows(35, 155, 35 + b[2] * 100, 155 + b[3] * 100, col = "red")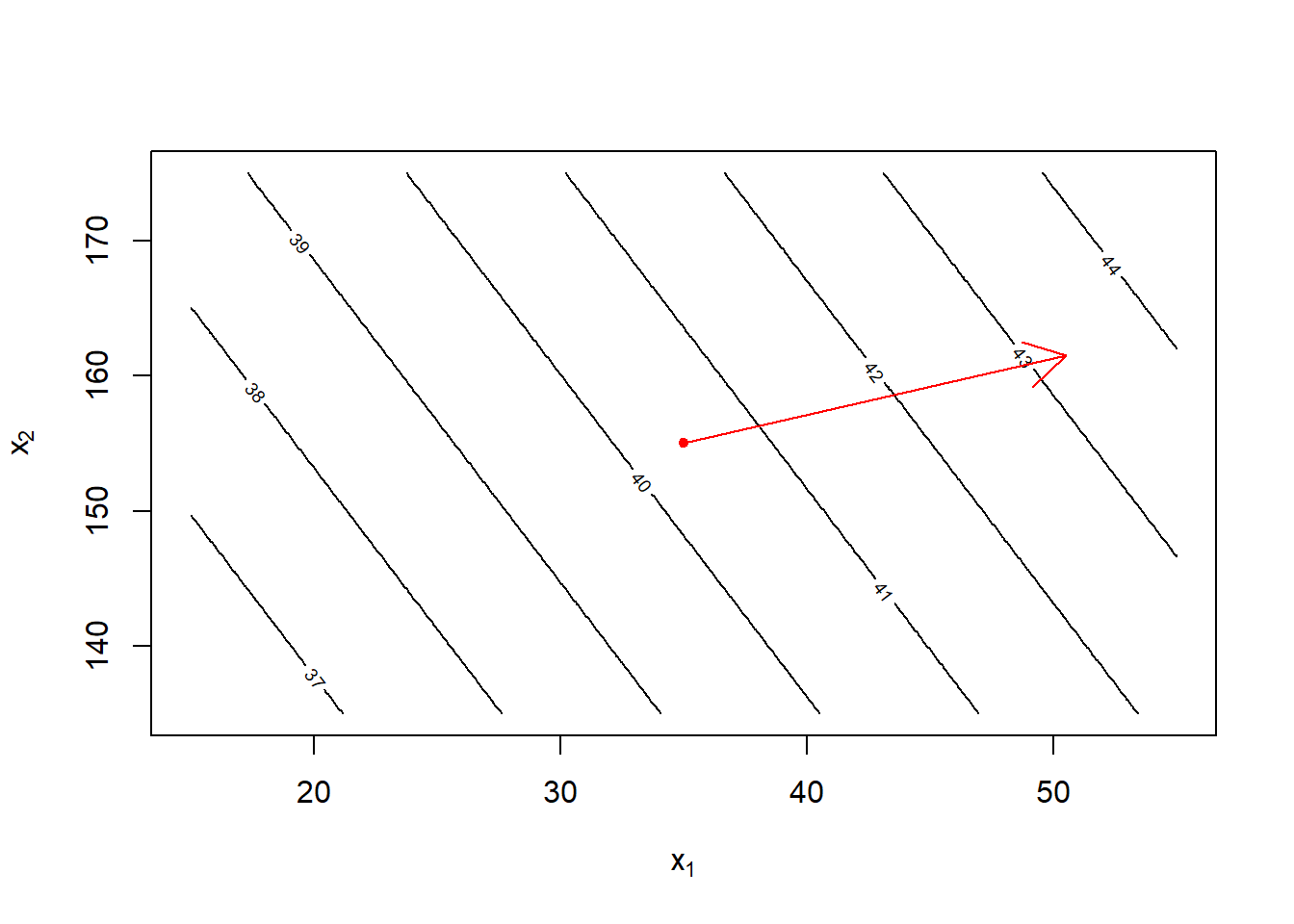

Se sperimentiamo lungo la retta indicata dal gradiente, muovendoci di piccoli passi, notiamo che la resa effettivamente aumenta per diversi passi per poi ricominciare a scendere. Prendiamo, ovviamente, la configurazione che restituisce la resa migliore tra quelle testate.

g <- b[-1]
names(g) <- c("dyhat/dx1", "dyhat/dx2")
Delta <- round(5 * g / max(abs(g)))
names(Delta) <- c("Delta1", "Delta2")
x <- c(X1 = 35, X2 = 155) ## configurazione corrente
ascesa <- NULL ## usato per memorizzare i risultati
x <- x + Delta
xy <- c(x, y = 41.0)
ascesa <- rbind(ascesa, xy)
# [tutti quelli intermedi, omessi per brevità...]
x <- x + 9*Delta
xy <- c(x, y = 80.3)
ascesa <- rbind(ascesa, xy)
x <- x + Delta
xy <- c(x, y = 76.2)
ascesa <- rbind(ascesa, xy)
ascesa
   X1  X2    y
xy 40 157 41.0
xy 85 175 80.3
xy 90 177 76.2

Nelle vicinanze del punto trovato è bene ripetere l’esperimento con un passo più fine, in modo da trovare più precisamente il punto di massimo. Il risultato dell’esperimento è la nuova matrice dei dati che considereremo.

## X1 X2
X <- matrix(
  c(
    80, 170,
    80, 180,
    90, 170,
    90, 180,
    85, 175,
    85, 175,
    85, 175,
    85, 175,
    85, 175
  ),
  9,
  byrow = TRUE
)
## y X1 X2
y <- c(
  76.5, # 80, 170
  77.0, # 80, 180
  78.0, # 90, 170
  79.5, # 90, 180
  79.9, # 85, 175
  80.3, # 85, 175
  80.0, # 85, 175
  79.7, # 85, 175
  79.8 # 85, 175
)

Un secondo modello è

m2 <- lm(y ~ I(X[, 1] - 85) + I(X[, 2] - 175))
summary(m2)

Call:
lm(formula = y ~ I(X[, 1] - 85) + I(X[, 2] - 175))

Residuals:
    Min      1Q  Median      3Q     Max 
-1.4667 -0.9667  0.7333  0.9333  1.3333 

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)      78.9667     0.4538 174.016 2.43e-12 ***
I(X[, 1] - 85)    0.2000     0.1361   1.469    0.192    
I(X[, 2] - 175)   0.1000     0.1361   0.735    0.490    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.361 on 6 degrees of freedom
Multiple R-squared:  0.3102,    Adjusted R-squared:  0.08023 
F-statistic: 1.349 on 2 and 6 DF,  p-value: 0.3283

I termini quadratici risultano significativi se aggiunti uno a uno, l’interazione ancora no. Non abbiamo abbastanza osservazioni per stimare il modello completo, dunque ne aggiungiamo di nuove. Il modello risulta

X.nuovi <- matrix(
c(
    92.07, 175.00,
    77.93, 175.00,
    85.00, 182.07,
    85.00, 167.93
  ),
  4,
  byrow = TRUE
)
## y X1 X2
y.nuovi <- c(
  78.4, # 92.07, 175.00
  75.6, # 77.93, 175.00
  78.5, # 85.00, 182.07
  77    # 85.00, 167.93
)

y <- c(y, y.nuovi)
X <- rbind(X, X.nuovi)
m3 <- lm(y ~ I(X[, 1] - 85) + I(X[, 2] - 175)
         + I((X[, 1] - 85) * I(X[, 2] - 175)) 
         + I((X[, 1] - 85)^2) + I((X[, 2] - 175)^2))
summary(m3)

Call:
lm(formula = y ~ I(X[, 1] - 85) + I(X[, 2] - 175) + I((X[, 1] - 
    85) * I(X[, 2] - 175)) + I((X[, 1] - 85)^2) + I((X[, 2] - 
    175)^2))

Residuals:
     Min       1Q   Median       3Q      Max 
-0.23995 -0.18089 -0.03995  0.17758  0.36005 

Coefficients:
                                    Estimate Std. Error t value Pr(>|t|)    
(Intercept)                        79.939955   0.119089 671.264  < 2e-16 ***
I(X[, 1] - 85)                      0.199010   0.018831  10.568 1.48e-05 ***
I(X[, 2] - 175)                     0.103041   0.018831   5.472 0.000934 ***
I((X[, 1] - 85) * I(X[, 2] - 175))  0.010000   0.005326   1.878 0.102519    
I((X[, 1] - 85)^2)                 -0.055058   0.004039 -13.630 2.69e-06 ***
I((X[, 2] - 175)^2)                -0.040053   0.004039  -9.916 2.26e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2663 on 7 degrees of freedom
Multiple R-squared:  0.9827,    Adjusted R-squared:  0.9704 
F-statistic: 79.67 on 5 and 7 DF,  p-value: 5.147e-06

La superficie del modello è

b <- coef(m3)
fhat <- function(x1, x2) {
  b[1] +b[2] * (x1 - 85) +
  b[3] * (x2 - 175) +
  b[4] * (x1 - 85) * (x2 - 175) +
  b[5] * (x1 - 85)^2 +
  b[6] * (x2 - 175)^2
}
x1 <- seq(65, 105, length = 200)
x2 <- seq(150, 200, length = 200)
yhat <- outer(x1, x2, fhat)

## Calcoliamo e disegnano il punto di massimo
B <- matrix(c(2 * b[5], b[4], b[4], 2 * b[6]), 2)
u <- c(85, 175) - solve(B, b[2:3])
c(X1.max = u[1], X2.max = u[2], yhat.a.X.max = fhat(u[1], u[2]))
                  X1.max                   X2.max yhat.a.X.max.(Intercept) 
                86.94615                176.52923                 80.21239 
contour(x1, x2, yhat, xlab = expression(x[1]), ylab = expression(x[2]))
points(u[1], u[2], cex = 2, pch = "*")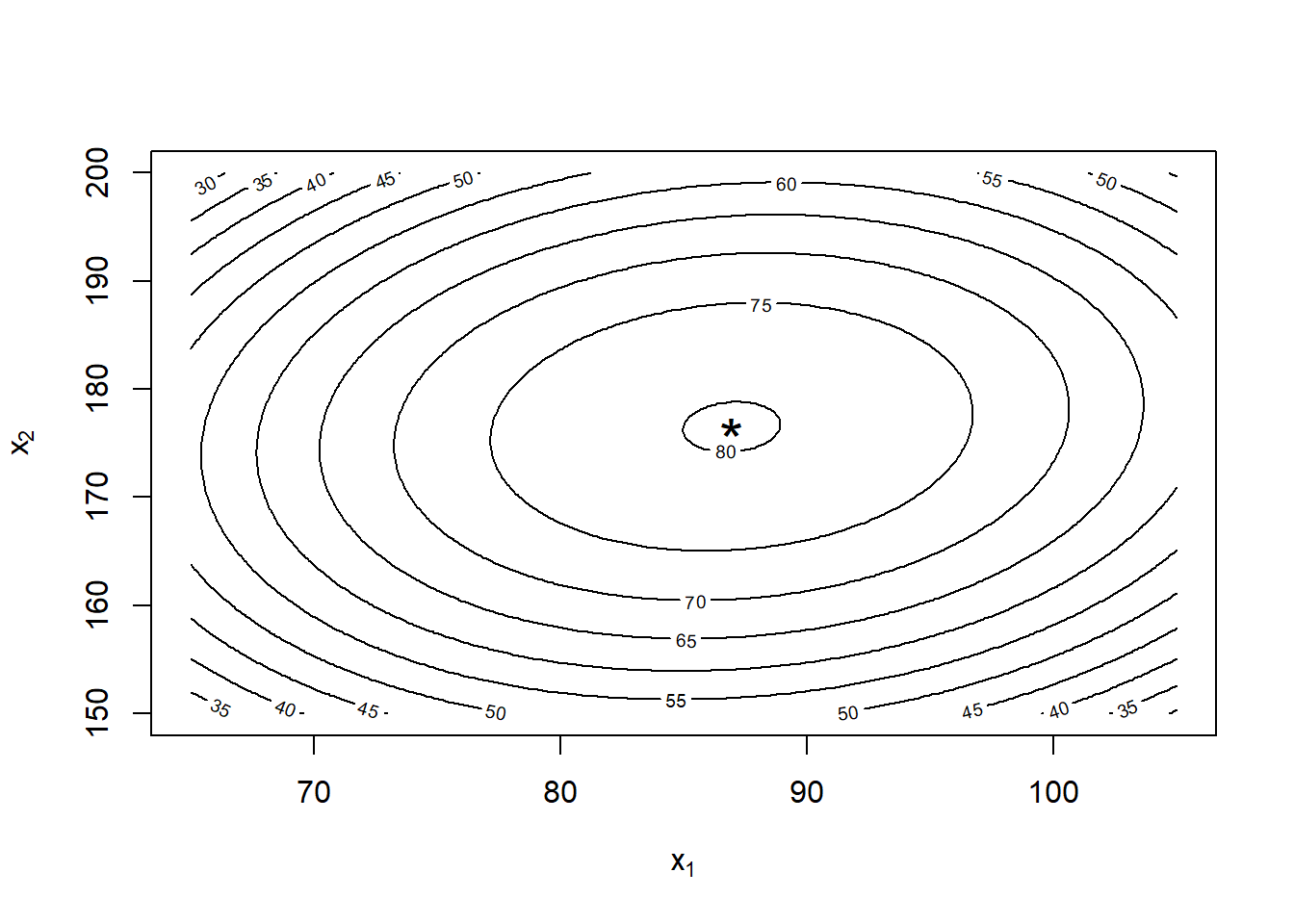

Calcolandoci il punto di massimo algebricamente, troviamo che la resa massima è in corrispondenza di \(X_1 \simeq 86.95m\), \(X_2 \simeq 176.5^\circ F\), come si vede anche dalle curve di livello. Il risultato atteso è un raddoppio della resa di ogni ciclo di produzione rispetto alla situazione pre-esperimento (anche se la durata di un ciclo è aumentata).

Caso 19: Dove cerchiamo di mettere sotto controllo il guadagno di alcuni transistor

In una industria di semiconduttori si vuole migliorare la performance della produzione, per cui il valore di \(y\) dovrebbe stare nell’intervallo di specifica \(200 \pm 20\), ma in questo momento il processo è poco capace. Sono presenti 5 concomitanti, \(X_1, X_2, X_3\) facilmente controllabili e \(Z_1, Z_2\) controllabili nella nostra fase di test nell’impianto pilota ma non durante l’effettiva produzione. Per ognuna di queste sono definiti due livelli, uno più alto e uno più basso, codificati come \(\pm 1\) a cui eseguire gli esperimenti. Si è eseguito un esperimento per ognuna delle \(2^5=32\) combinazioni delle esplicative e si è registrato il valore di \(y\) corrispondente. Si vuole capire come regolare le esplicative \(X_1, X_2, X_3\) in modo da mantenere \(y\) con media 200 e variabilità più piccola possibile, anche considerando \(Z_1, Z_2\).

d <- read.table("~/Uni/Controllo/Datasets/gain")
str(d)
'data.frame':   32 obs. of  6 variables:
 $ x1: int  -1 -1 -1 -1 1 1 1 1 -1 -1 ...
 $ x2: int  -1 -1 -1 -1 -1 -1 -1 -1 1 1 ...
 $ x3: int  -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
 $ z1: int  -1 1 -1 1 -1 1 -1 1 -1 1 ...
 $ z2: int  -1 -1 1 1 -1 -1 1 1 -1 -1 ...
 $ y : num  130 112 125 118 158 ...
summary(m1 <- lm(y ~ (x1 + x2 + x3 + z1 + z2)^2, data = d))

Call:
lm(formula = y ~ (x1 + x2 + x3 + z1 + z2)^2, data = d)

Residuals:
     Min       1Q   Median       3Q      Max 
-10.9425  -2.6725   0.5525   3.3569   6.5825 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 187.9837     1.0446 179.956  < 2e-16 ***
x1           15.4944     1.0446  14.833 9.04e-11 ***
x2           24.7475     1.0446  23.691 6.93e-14 ***
x3            9.8850     1.0446   9.463 5.89e-08 ***
z1            5.6319     1.0446   5.391 6.00e-05 ***
z2            1.3675     1.0446   1.309    0.209    
x1:x2        -8.6519     1.0446  -8.282 3.53e-07 ***
x1:x3        -8.0144     1.0446  -7.672 9.50e-07 ***
x1:z1        16.9887     1.0446  16.263 2.26e-11 ***
x1:z2         1.6219     1.0446   1.553    0.140    
x2:x3         0.0300     1.0446   0.029    0.977    
x2:z1        -6.4981     1.0446  -6.221 1.22e-05 ***
x2:z2        -0.8675     1.0446  -0.830    0.419    
x3:z1         0.1094     1.0446   0.105    0.918    
x3:z2         0.4200     1.0446   0.402    0.693    
z1:z2        -0.7231     1.0446  -0.692    0.499    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.909 on 16 degrees of freedom
Multiple R-squared:  0.9882,    Adjusted R-squared:  0.9771 
F-statistic: 89.07 on 15 and 16 DF,  p-value: 1.594e-12
summary(m2 <- lm(y ~ (x1 + x2 + x3 + z1)^2, data = d))

Call:
lm(formula = y ~ (x1 + x2 + x3 + z1)^2, data = d)

Residuals:
    Min      1Q  Median      3Q     Max 
-8.8025 -2.8719 -0.1556  3.2156  8.3150 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 187.9837     1.0559 178.038  < 2e-16 ***
x1           15.4944     1.0559  14.675 1.64e-12 ***
x2           24.7475     1.0559  23.438  < 2e-16 ***
x3            9.8850     1.0559   9.362 6.07e-09 ***
z1            5.6319     1.0559   5.334 2.74e-05 ***
x1:x2        -8.6519     1.0559  -8.194 5.59e-08 ***
x1:x3        -8.0144     1.0559  -7.590 1.89e-07 ***
x1:z1        16.9887     1.0559  16.090 2.76e-13 ***
x2:x3         0.0300     1.0559   0.028    0.978    
x2:z1        -6.4981     1.0559  -6.154 4.17e-06 ***
x3:z1         0.1094     1.0559   0.104    0.918    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.973 on 21 degrees of freedom
Multiple R-squared:  0.9841,    Adjusted R-squared:  0.9766 
F-statistic: 130.2 on 10 and 21 DF,  p-value: < 2.2e-16
summary(m3 <- lm(y ~ (x1 + x2 + x3 + z1)^2 - x2:x3 - x3:z1, data = d))

Call:
lm(formula = y ~ (x1 + x2 + x3 + z1)^2 - x2:x3 - x3:z1, data = d)

Residuals:
    Min      1Q  Median      3Q     Max 
-8.8819 -2.9662 -0.1556  3.3100  8.1756 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  187.984      1.009 186.273  < 2e-16 ***
x1            15.494      1.009  15.353 1.40e-13 ***
x2            24.747      1.009  24.522  < 2e-16 ***
x3             9.885      1.009   9.795 1.13e-09 ***
z1             5.632      1.009   5.581 1.12e-05 ***
x1:x2         -8.652      1.009  -8.573 1.28e-08 ***
x1:x3         -8.014      1.009  -7.941 4.86e-08 ***
x1:z1         16.989      1.009  16.834 1.99e-14 ***
x2:z1         -6.498      1.009  -6.439 1.43e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.709 on 23 degrees of freedom
Multiple R-squared:  0.9841,    Adjusted R-squared:  0.9786 
F-statistic: 178.2 on 8 and 23 DF,  p-value: < 2.2e-16
anova(m3, m1, test = "F")
Analysis of Variance Table

Model 1: y ~ (x1 + x2 + x3 + z1)^2 - x2:x3 - x3:z1
Model 2: y ~ (x1 + x2 + x3 + z1 + z2)^2
  Res.Df    RSS Df Sum of Sq     F Pr(>F)
1     23 749.58                          
2     16 558.70  7    190.89 0.781 0.6125
confint(m3)
                 2.5 %     97.5 %
(Intercept) 185.896089 190.071411
x1           13.406714  17.582036
x2           22.659839  26.835161
x3            7.797339  11.972661
z1            3.544214   7.719536
x1:x2       -10.739536  -6.564214
x1:x3       -10.102036  -5.926714
x1:z1        14.901089  19.076411
x2:z1        -8.585786  -4.410464

Il modello completo non è significativamente migliore di quello semplificato, dunque quest’ultimo è preferibile. Non vi sono indicazioni contro la normalità dei residui.

Riportando le esplicative alla scala originale otteniamo che \(E[y|x_1,x_2,x_3] \simeq 188\) e \(sd(y|x_1,x_2,x_3) = \sqrt{\beta_5^2+\sigma_\varepsilon^2} \simeq 8.02\), non soddisfacente in quanto la coda di sinistra sta quasi del tutto fuori dai limiti di specifica. Si noti che \(Z_1\) è una variabile casuale assunta normale, per cui la varianza della risposta del modello non dipende solo, com’è usuale, da \(\sigma^2_\varepsilon\), ma anche dai coefficienti di \(Z_1\) \(\beta_5, \beta_8 \text{ e } \beta_9\).

L’indice \(C_{pk}\) fa abbastanza ridere

mu_attuale <- coef(m3)[1]
sigma_epsilon <- sqrt(sum(residuals(m3)^2) / m3$df.resid)
                 # beta_5 è il coeff. di z_1
sigma_attuale <- sqrt((coef(m3)[5])^2 + sigma_epsilon^2)
LSL <- 200 - 20
USL <- 200 + 20
(mu_attuale - LSL) / (3 * sigma_attuale)
(Intercept) 
   0.331857

Per migliorare la capacità del processo possiamo utilizzare le interazioni tra \(Z_1\) e le variabili che possiamo controllare. Si veda il laboratorio per i calcoli.

curve(dnorm(x, 200, sigma_epsilon), 160, 240,
col = 3, lwd = 2
)
curve(dnorm(x, mu_attuale, sigma_attuale), 160, 240,
col = 4, lwd = 2, add = TRUE
)
grid()
abline(v = LSL, col = 2, lty = "dotted", lwd = 2)
abline(v = USL, col = 2, lty = "dotted", lwd = 2)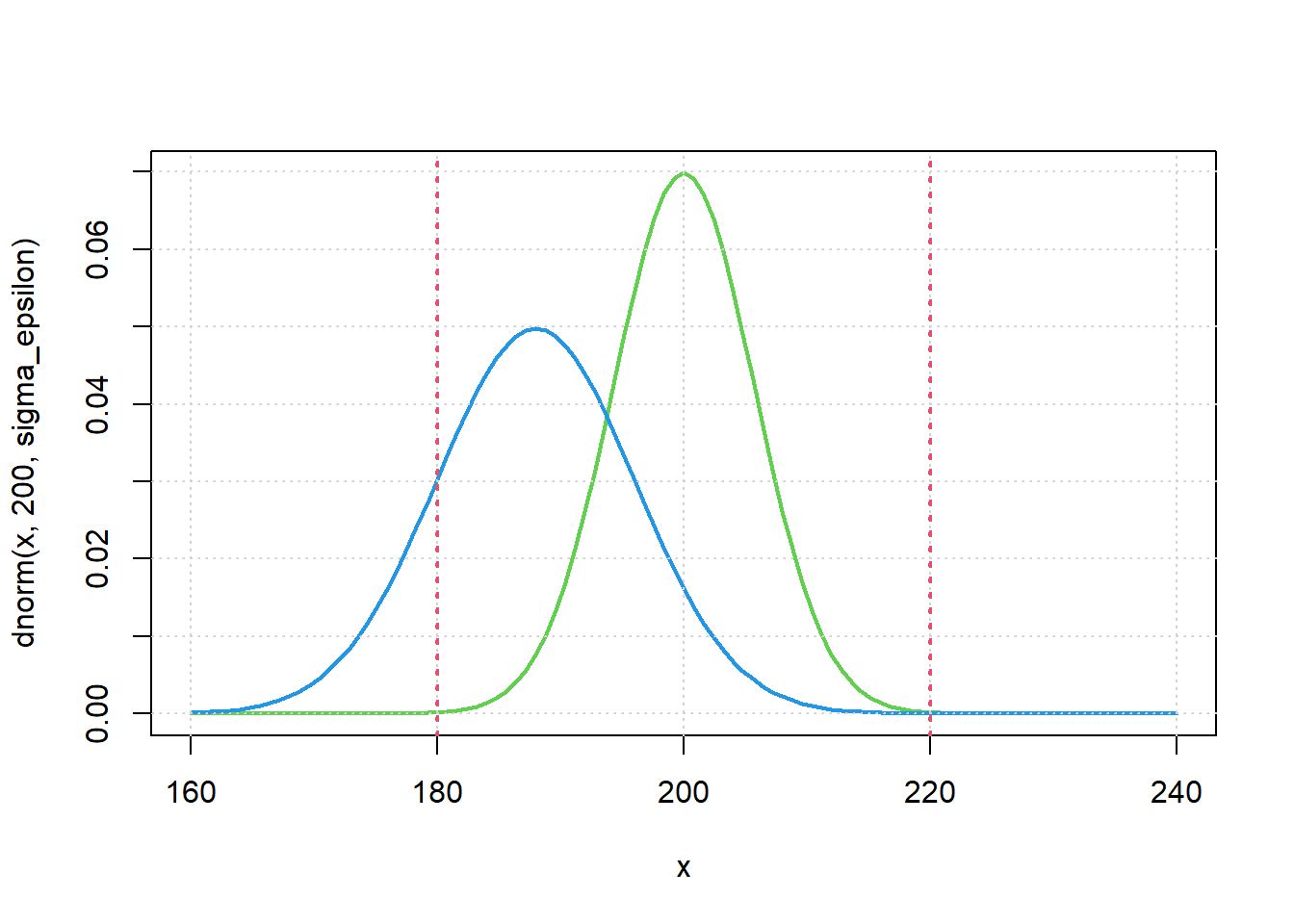

(USL - LSL) / (6 * sigma_epsilon)
[1] 1.167784

La nuova distribuzione e la relativa capacità sono ora decenti. In questo contesto è importante considerare simultaneamente tutti i fattori che influenzano la risposta ed il loro effetto sia sulla posizione che sulla variabilità della risposta. Lo stesso risultato, infatti, non si sarebbe potuto ottenere modificando solo una delle esplicative.

Caso 20: Sul controllo della CO2 in una fornace a gas

I dati costituiscono una serie temporale bivariata, raccolta ad intervalli di 9 secondi in una fornace a gas metano usata per forgiare piccoli oggetti di metallo. \(y\) indica la quantità percentuale di \(CO_2\) all’interno della fornace (caratteristica da controllare), mentre \(x\) il flusso di metano immesso nell’impianto, che è un valore facilmente manipolabile a piacere (ovvero, è una covariata che ha effetto su y).

d <- read.table("~/Uni/Controllo/Datasets/fornace-gas", header = TRUE)
str(d)
'data.frame':   296 obs. of  2 variables:
 $ y: num  53.8 53.6 53.5 53.5 53.4 53.1 52.7 52.4 52.2 52 ...
 $ x: num  0.604 0.6 0.593 0.586 0.585 ...
plot(ts(d, frequency=1/9), main="", xlab="Secondi")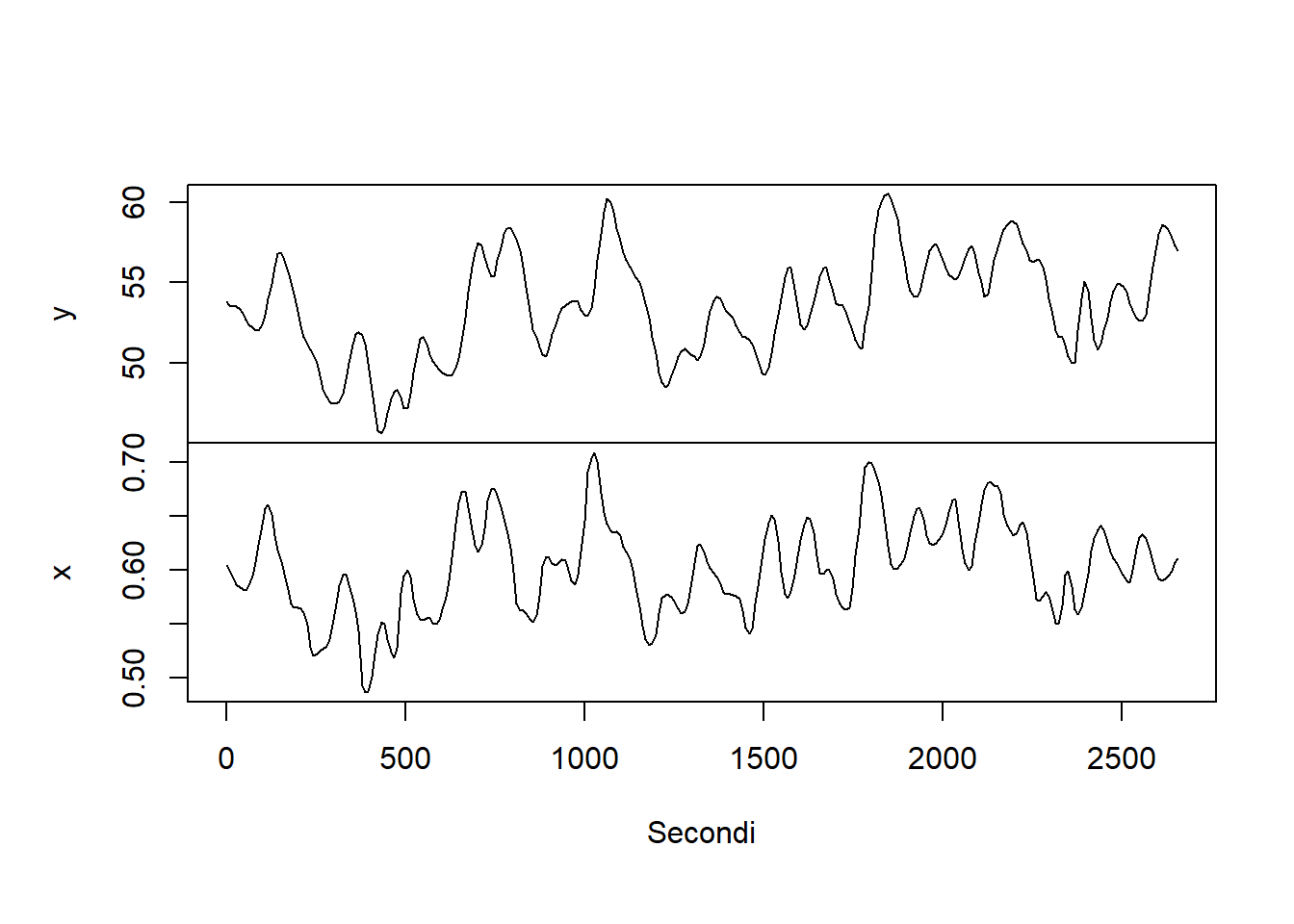

acf(d, ylim=c(-1,1))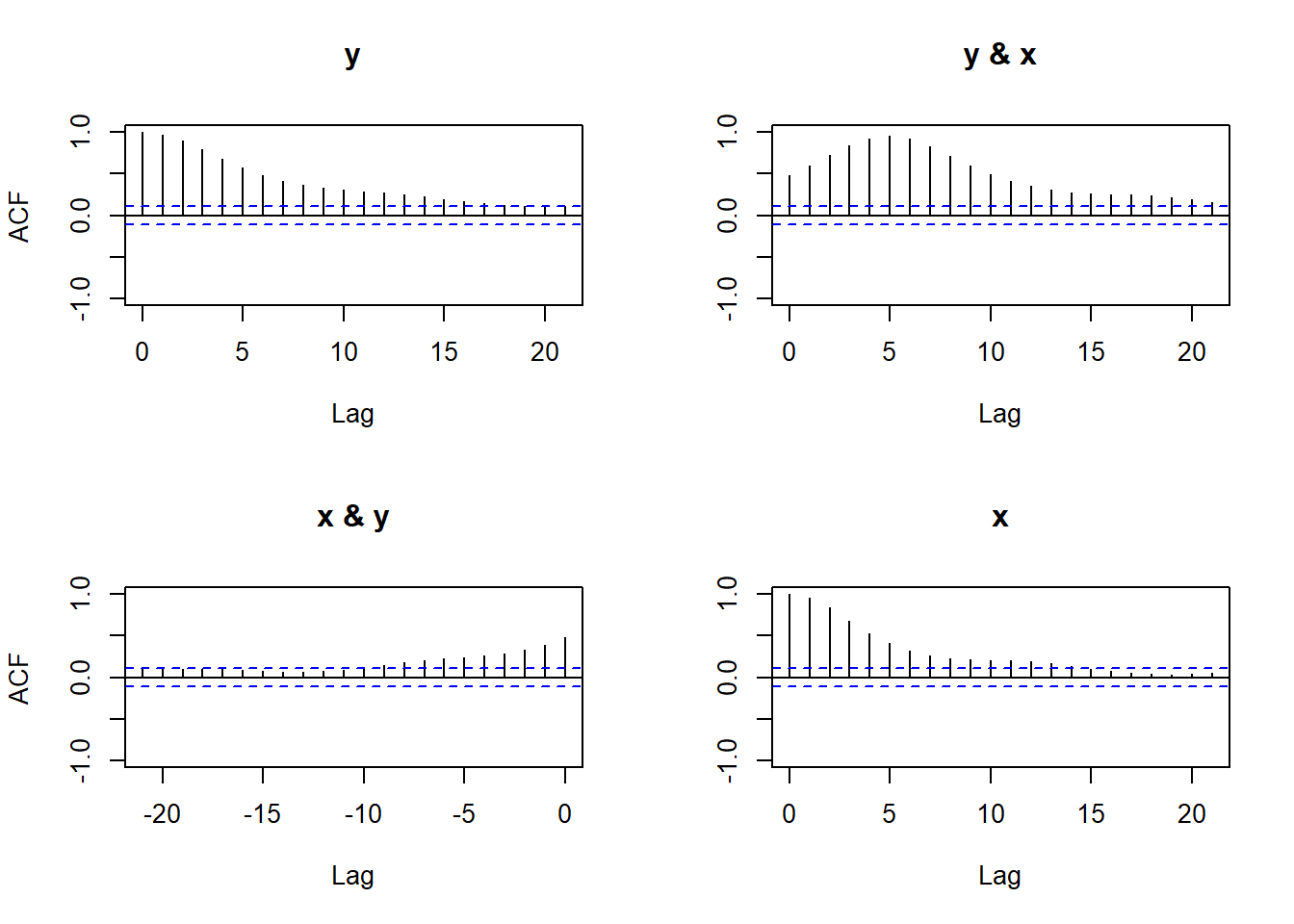

Si evidenzia forte autocorrelazione semplice e incrociata. Possiamo utilizzare un modello ARX(p,r) secondo cui il modello generatore dei dati è \[ y_t = \beta_0 + \sum_{i=1}^{p} \beta_i y_{t-i} + \sum_{i=0}^{r} \beta_{p+1+i} x_{t-i} + \varepsilon_t \]

Basandoci sul picco dell’ACF tra \(y\) e \(x\), proviamo intanto un ARX(6,6)

idx <- 7:NROW(d)
m <- lm(y[idx]~y[idx-1]+y[idx-2]+y[idx-3]+y[idx-4]+y[idx-5]+y[idx-6]+
        x[idx]+x[idx-1]+x[idx-2]+x[idx-3]+x[idx-4]+x[idx-5]+x[idx-6],
        data=d)
summary(m)

Call:
lm(formula = y[idx] ~ y[idx - 1] + y[idx - 2] + y[idx - 3] + 
    y[idx - 4] + y[idx - 5] + y[idx - 6] + x[idx] + x[idx - 1] + 
    x[idx - 2] + x[idx - 3] + x[idx - 4] + x[idx - 5] + x[idx - 
    6], data = d)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.75746 -0.12607 -0.02329  0.11034  1.40743 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.31913    0.30051   1.062   0.2892    
y[idx - 1]   1.54181    0.05996  25.714  < 2e-16 ***
y[idx - 2]  -0.58621    0.11056  -5.302 2.35e-07 ***
y[idx - 3]  -0.17642    0.11539  -1.529   0.1274    
y[idx - 4]   0.13419    0.11472   1.170   0.2431    
y[idx - 5]   0.05408    0.10092   0.536   0.5925    
y[idx - 6]  -0.04003    0.04297  -0.932   0.3524    
x[idx]       1.68310    1.92014   0.877   0.3815    
x[idx - 1]  -4.82963    4.16704  -1.159   0.2475    
x[idx - 2]   5.36367    4.72853   1.134   0.2576    
x[idx - 3]  10.74528    4.73057   2.271   0.0239 *  
x[idx - 4]  -3.53056    4.76732  -0.741   0.4596    
x[idx - 5]   2.36919    4.54634   0.521   0.6027    
x[idx - 6]  -5.87303    2.77514  -2.116   0.0352 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2415 on 276 degrees of freedom
Multiple R-squared:  0.9947,    Adjusted R-squared:  0.9944 
F-statistic:  3969 on 13 and 276 DF,  p-value: < 2.2e-16

È evidentemente opportuno semplificare il modello. Siccome non c’abbiamo voglia, teniamo direttamente solo le esplicative già significative.

m1 <- lm(y[idx]~y[idx-1]+y[idx-2]+x[idx-3]+x[idx-6], data=d)
summary(m1)

Call:
lm(formula = y[idx] ~ y[idx - 1] + y[idx - 2] + x[idx - 3] + 
    x[idx - 6], data = d)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.99115 -0.11880 -0.01356  0.11575  1.40218 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.53603    0.27015   1.984   0.0482 *  
y[idx - 1]   1.44560    0.03303  43.764  < 2e-16 ***
y[idx - 2]  -0.51434    0.02583 -19.910  < 2e-16 ***
x[idx - 3]  12.73443    0.64938  19.610  < 2e-16 ***
x[idx - 6]  -7.50637    1.11010  -6.762  7.7e-11 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2456 on 285 degrees of freedom
Multiple R-squared:  0.9943,    Adjusted R-squared:  0.9942 
F-statistic: 1.247e+04 on 4 and 285 DF,  p-value: < 2.2e-16
acf(residuals(m1), ylim=c(-1,1))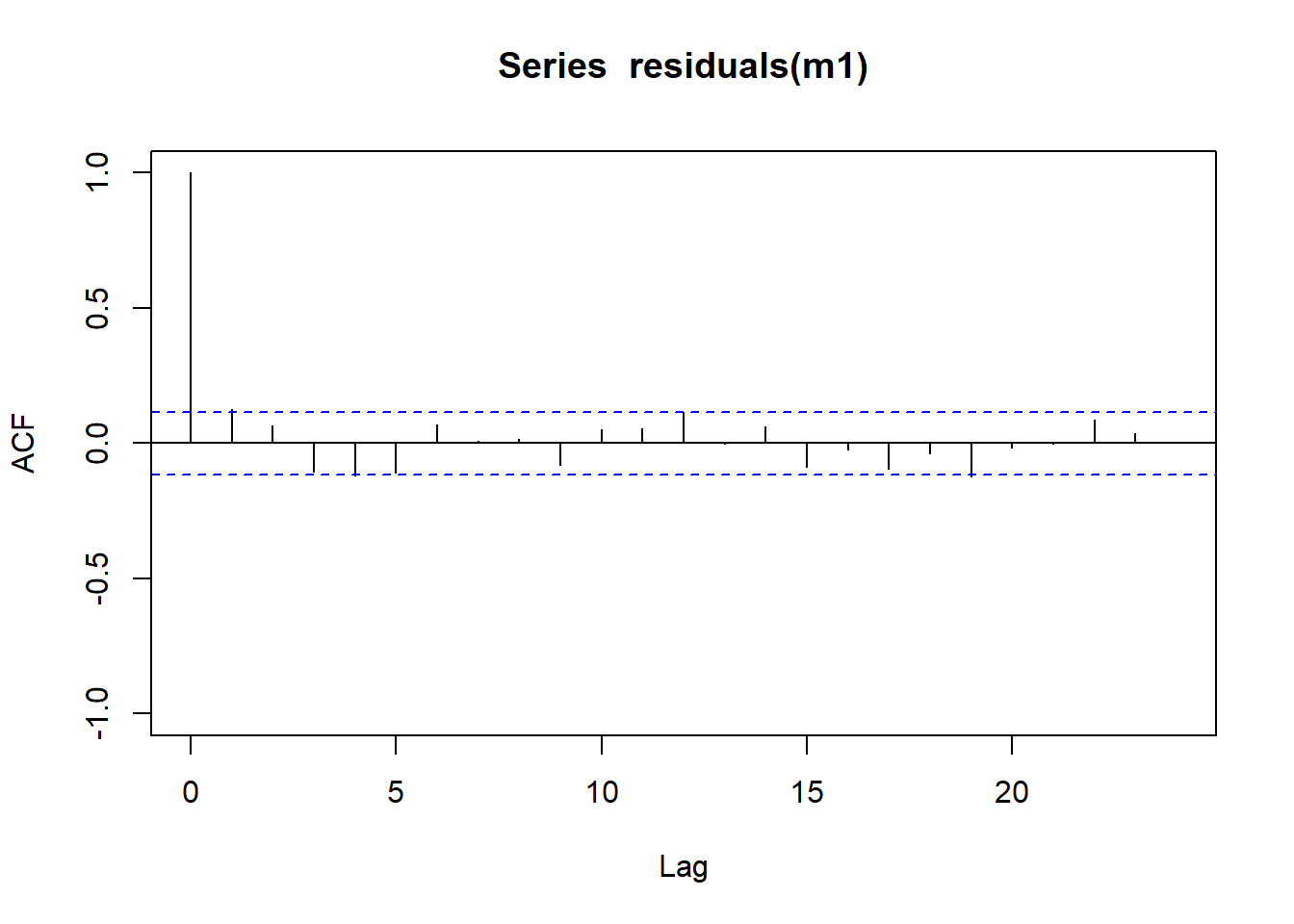

ccf(residuals(m1), d$x[idx], ylim=c(-1,1))  # cross-correlation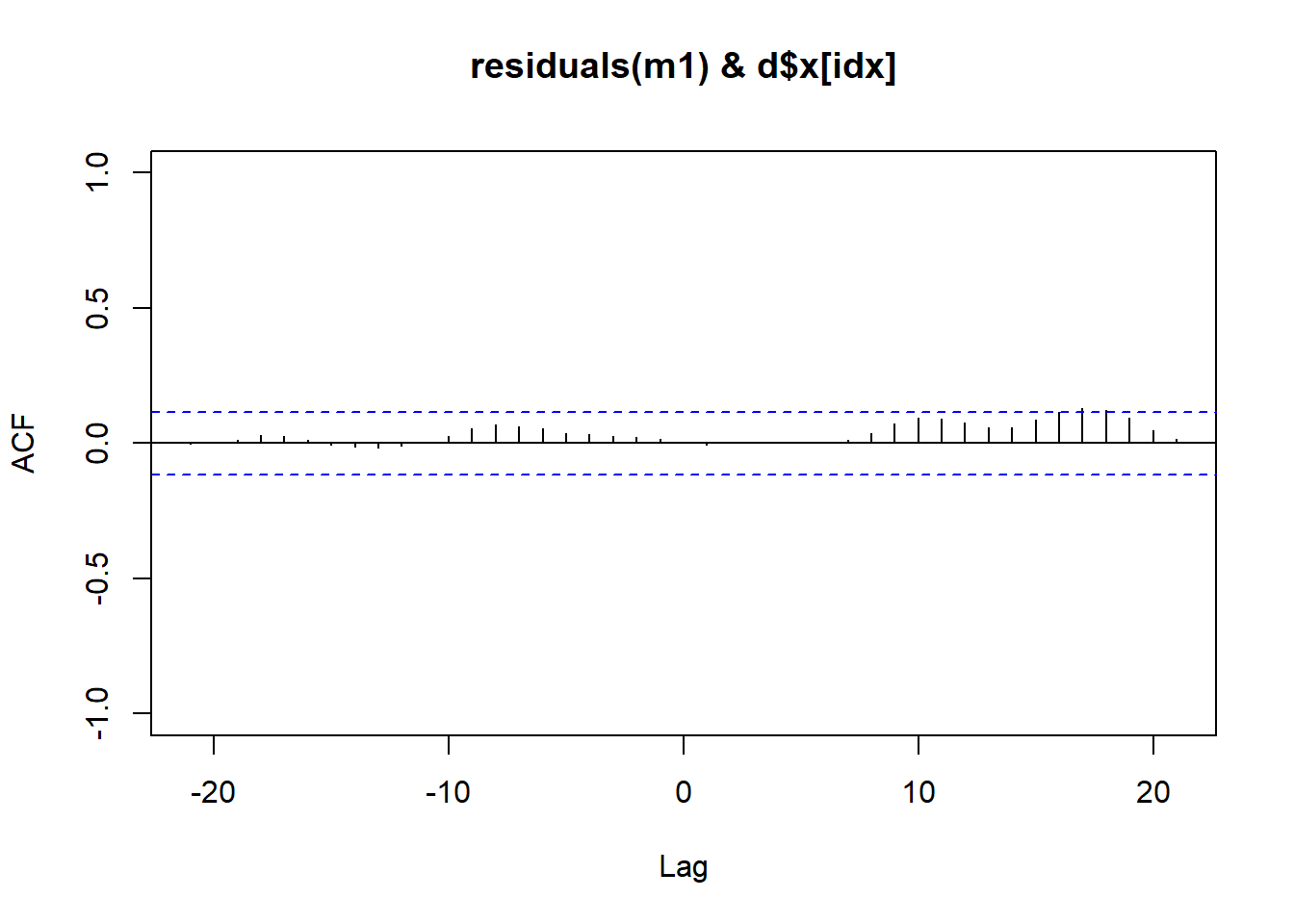

Il modello è accettabile. Si ha dunque \[ y_t = \beta_0 + \beta_1 y_{t-1} + \beta_2 y_{t-2} + \beta_3 x_{t-3} + \beta_4 x_{t-6} + \varepsilon_t \] Da cui banalmente le stime. Si noti dunque che la variazione di \(x\) impatta la \(y\) con un certo lag temporale.

Una prima strategia di manipolazione della \(x\) è quella di settarla ad un livello costante \(\xi\), in modo che \(\eta = E[y_t]\) balli intorno al valore desiderato. Siccome il livello è costante, otteniamo semplicemente \[ \eta = \beta_0 + \beta_1 \eta + \beta_2 \eta + \beta_3 \xi +\beta_4 \xi \] e dunque scegliamo il valore a cui fissare \(x\) dai valori stimati per i parametri del modello precendente, come \[ \hat{\xi} = \frac{\eta(1 - \hat{\beta}_1 - \hat{\beta}_2) - \hat{\beta}_0}{\hat{\beta}_3 + \hat{\beta}_4} \] In sostanza, si può verificare che otteniamo il seguente modello AR(2): \[ y_t = \eta + \beta_1 (y_{t-1} - \eta) + \beta_2 (y_{t-2} - \eta) + \varepsilon_t \]

Siccome è possibile nel nostro caso modificare quasi istantaneamente il valore di \(x\) a costo nullo, è sensato modificare il flusso di metano ad ogni nuova osservazione di \(y_t\). Vogliamo minimizzare il MSE tra \(y_t\) e il valore target \(\eta\). I calcoli sono noiosi, ma il concetto è che al momento dell’osservazione di \(y_t\) modifichiamo il valore di \(x_t\) in modo tale che la previsione di \(y_{t+3}\) sia esattamente uguale al valore target. \(y\) ha un lag di 3 osservazioni (27 secondi) rispetto ad una modifica di \(x\), dunque il valore osservato di \(y_{t+3}\) risentirà di tutti i termini d’errore successivi.

Per la sorveglianza del processo, l’azienda utilizza una carta CuSum su \(\varepsilon_t\) invece che su \(y_t\).